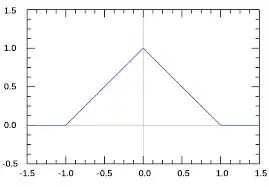
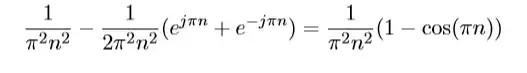I want to evaluate the Fourier series expansion of $ x_1(t) = \sum _{-\infty}^{\infty} \Delta (t-2n) $, where $ \Delta (t) $ is a triangular function defined as:
I have done the following calculations so far. However, two of these six terms need to cancel. But as per my calculations, all the six terms are retained. The answer should be:
I have enclosed my solution below:
I think there's some sort of minor mistake in my solution.