How Do I Measure the Time Duration of a Finite Length Discrete Sequence?

Question

Assume I have a five-sample time-domain sequence (none of the five samples are zero valued) and the time period between each pair of samples is one second. Measured in seconds, what is the time duration of my five-sample sequence?

Answer 1

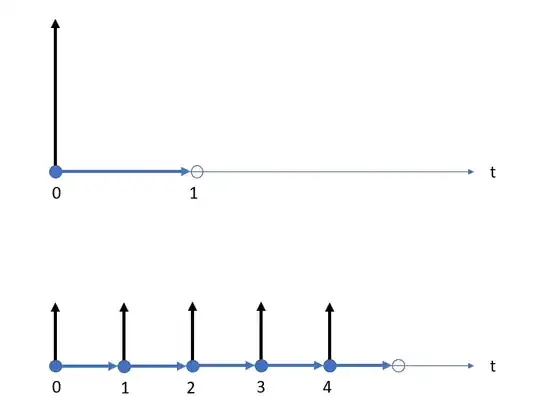
The following graphic should clear up why a useful answer is 5 seconds, consistent with conversions between the discrete-time and continuous-time domains. A good example of this are discrete time approximations to continuous time integration or differentiation where the inclusion of $\Delta T$ (sample period) is made. With all such approximations, the time duration attributed to each sample is one sample interval. For the Forward Euler approximation specifically, each sample covers the time duration up to and not including the next sample. Such as in the first graphic the time duration for a sample at $t=0$ is one sample interval of one second; up to and not including the next sample at $t=1$ when sampled at one sample per second, with a total time duration for the one sample as one second.

The bottom figure then shows how this would apply to five samples starting at $t=0$ resulting in a total time duration of 5 seconds.

The plot below shows the Forward Euler discrete-time approximation for the integration of a continuous time waveform $x(t)$, which would be given as follows in the formula below and demonstrated in the graphic, best showing how each sample carries the time duration of the sample period (and as David has pointed out in the comments, this equally represents the zero-order hold approach in the output of a typical Digital to Analog converter):

$$\int_0^{NT}x(t)dt \approx \sum_{n=0}^{N-1}x[n]T$$

The actual range of time used for each sample is specific to the analog-digital translation approach used, but would cover one sample duration in all cases, leading to a total duration of 5 seconds for the OP's case.

Answer 2

By the way, "measure" isn't quite the right term here: you're not measuring a physical quantity, but that would be nitpicking; a sequence doesn't have duration. (You have another question that also touches upon that, and I always found it helpful to remind myself that a sequence like 0.1, 0.3, -0.2, 0.0, 1.0 has no duration, as it's just a bunch of numbers in order. Duration is an attribute we infer from it representing something, which usually doesn't matter for the math we do on the sequence.)

The continuous-time signal it represents has a duration! So, let's look at that.

So, first of all, we need to make an assumption: your signal is bandwidth-limited – otherwise sampling it had made no sense.

Then: we need to assume that it's periodically repeating! Otherwise, you don't get to claim that your DFT is representative of your continuous signal's spectrum (only periodic signals have line spectra).

And then you're right, your signal repeats every 5 sample periods.

If we take away the assumption that the underlying time-continuous signal is periodic, we end up in a hard situation: We have a signal that is strictly bandlimited, so it can't be finite in duration!

A good reminder of that is the reconstruction theorem, where we interpolate all the samples we have with sinc. The nice thing about that is that each sinc is zero at all but one sample instant (where it takes the value of the sample).
The less nice thing about that is that a sinc never truly stays zero. (Look at Dan Boschen's integral figure and replace the rectangles with sincs centered at each sample instant. When do the sincs disappear? Never!)

And thus I think, the real answer (applying Occam's razor of using as few assumptions as necessary) is that

• you have no signal duration without interpreting your sequence as representation of something else
• if you do that interpretation of the sequence as samples from a bandlimited signal, then the signal that effected these samples is infinite in duration,
• if you do that interpretation of the sequence as samples from a bandlimited, periodic signal, then only periods of five sample instants make sense. (and it's still infinite)

So, in any case, if we assign an attribute "length" to this sequence, strictly speaking, it'd be infinite.

Answer 3

The OP's query and his response to Laurent Duval's comment is very reasonable and the OP's question should not be closed. See the answer by Richard Lyons (author of the well-regarded book Understanding Digital Signal Processing) to this question. Richard now concludes that the OP's second choice (that the signal duration of a 5-sample discrete-time signal with one sample per second is 5 seconds) is correct, and that the notion that the first and last samples are separated by only 4 seconds and hence the signal duration is 4 seconds is not appropriate.

Answer 4

I hope this is clear and helpful.

Given a continuous-time signal $x_a(t)$, if you perform an ideal impulse-train modulation based uniform sampling of it by a sampling period of $T_s$ seconds as indicated by:

$$x[n] = x_a(t_n) = x_a(n T_s) $$

and obtain $N$ such samples, then the duration of your observation is given by :

$$ \Delta T = (N-1)\cdot T_s $$

The time-stamp of the first sample $x[0]$ will be at $t_0 = 0\cdot T_s =0$ and the time-stamp of the last sample $x[N-1]$will be at $t_{N-1} = (N-1)\cdot T_s$.

Nevertheless, in some applications (such as sample rate conversion) it's customary to call the duration as $\Delta T = N \cdot T_s$, by adding one more period $T_s$ that spans after the last taken sample $x[N-1]$ and the next un-taken sample at time $t_N = N \cdot T_s$.

Answer 5

I throw another on in the mix:

The question is oddly worded but my interpretation is "I have a 5 point discrete sequence sampled at $1Hz$, what's the length of the corresponding continuous time domain signal in seconds".

First we need to define what we mean by "corresponding". In order for the sequence to completely capture a continuous signal, this signal must be bandlimited. So if we require our sequence to represent a complete description of the corresponding continuous signal, the length of that signal must be infinite. (Since all band limited signals have inifinite lengths)

If we allow for aliasing, then the length is "whatever you want it to be". There is an inifite number of continuous signals that would result in our original sequence when sampled. In other words, for any given time length you can construct a continuous signal that will sample as our original sequence.

EDIT:

So it seems like I misinterpreted the question. OP wants to know ""what is the time duration of my five-sample sequence?"

The answer to this is: it doesn't have any. The length is $5$ (no units) and that's that.

In order to define time length as a physcial quantity you need to create a physical manifestation of that discrete sequence. In other words, you need to run it through a D/A converter and then you can measure actual physical time. The result of this measurement will be dependent on the implementationd details of the D/A. D/A create compromise between "time smearing" and "aliasing" An "ideal" D/A converter would create a signal that's infinitely long, but of course, that's impossible and impractical.

We are having some fun philosphical discussion on this topic with fairly different opinions. Now that would be all futile, if you could simply measure it, but it turns out there is no well defined "time length" that's measurable and would provide the definitive answer.

Answer 6

I would answer $4+\epsilon$ seconds. Because Richard Hamming, one of my (our?) godfather is credited with this "The purpose of computing is insight, not numbers". As commented by many, precise definitions and usefulness are necessary.

Before explanations, let me play on terms, and propose a first (silly?) answer. Thus, my first answer is:

$$\frac{1}{24}\; \textrm{second}^4\,.$$

Yes, in seconds to the fourth power. Indeed, if the time period between each pair of samples is one second, the simplest geometrical structure allowing five points to be equidistant is the pentatope, or Four-Simplex. This is the simplest polytope in a four-dimensional space. In 1D, two points can be separated by one second. For three points, one needs to place a equilateral triangle in the plane. With four points, a tetrahedron, and so on. The hypervolume of a pentatope with vertices $(0,0,0,0)$ ,$(a,0,0,0)$ ,$(0,b,0,0)$ ,$(0,0,c,0)$ ,$(0,0,0,d)$ is $\frac{abcd}{24}$, see Hypervolume of the 4-simplex. This would suppose that we live in a time-space with at least four time dimensions, a bit too much for the stability of the laws of the Universe. This was meant to emphasize on how far people could go on things as "natural" as each pair.

Going back to 1D. The question is about a "five-sample time-domain sequence". To me, not a signal per se, while it might represent some signal, continuous or discrete, whose acquisition method is not specified (yet). The mention of time in second can be misleading, only providing a unit to the $x$-axis. Let us rely on the notions of support from mathematics. As you can see, people tried to define unambiguous definitions, and there are many. As a pure sequence, the set-theoretic support of the sequence is finite. The closed support (intersection of all closed sets that contain the set-theoretic support) and compact support would be the same interval $[0,4]$ in seconds. Its essential support would be of length $0$.

For signal processing, I understand the idea that each sample is related to some interval of one second (hence the 5-second length answer). And I voted for Dilip Sarwate's answer, which means that this question is still triggering my mind. However, after a second thought, I have no idea about the way the original signal was sampled: maybe the last sample was averaged over 2 seconds, while the first one had "instantaneous capture". The fact that "The time period between [consecutive] samples is one second" may be a choice of storage, an artifact, a result for compresive sensing, etc.

In other words, I don't know if some hypothetical signal was regularly sampled. So with minimal hypotheses, another side of the Ockham razor evoked elsewhere, I would consider that if it was indeed sampled in the real world, it can be imperfect, because of integration time, or jitter, and I'd allow some uncertainty $\epsilon \ge 0$. Hence, my present answer is:

$$ 4+\epsilon\,.$$

on my most solid grounds. At least, something to discuss openly.

Answer 7

I've pondered a better take on this; "what is the duration?" can ask two separate questions:

1. For how long have we been sampling?
2. How much time's worth of information is contained in our signal?

I'd argue the answers to these are, unambiguously, $(N - 1)/f_s$ and $N/f_s$, respectively. To interpret either, I'll refer to following sampling times: $t=[0, .1, .2, .3, .4, .5, .6, .7, .8, .9] \text{sec}$.

---

1. For how long have we been sampling?

We begin with first sample. At that time, no time has passed, else we wouldn't be "at that time" but at later time, so we've been sampling for a total of 0 sec. At next sample, 0.1 sec have passed since we began sampling - so we've been sampling for 0.1 sec. And so on: total duration = 0.9 sec.

2. How much time's worth of information is contained in the signal?

The answer to this is either 0 sec or 1 sec. Refer to other answers, but basically there's agreement that the sequence is representative of physical source process in one of below senses:

Black arrows are values of observations we draw from a system (purple), and blue lines (white gaps for clarity) are time intervals spanned by observations.

Which is "better", A or B? Well, with B, we're saying the observation at $t=.1$ "speaks for" the process for $t=[.1, .2)$, where with A we're saying it represents $t=[.05, .15)$.

• Note for $t=.3$, B fares better, since values within $[.3, .4)$ are much closer on average to value at $t=.3$, than values within $[.25, .45)$. If we shifted the whole process left by $.05 \text{sec}$, A fares better. Point is, we just defined "better" as "more representative", which we measured as "less variance".
• B is more akin to "speaking for the future" than A is, and "reverse B" where blue line is drawn all the way left is guilty of "speaking for past". In this sense, A is the optimal scheme in localizing observations.

---

Example 1: take an "instant thermometer" and sample a lake's temperature every 30 minutes, 6 times.

• For how long have we been sampling? We started at 6AM, finished at 8:30AM --> 2.5 hours.
• How much time's worth of information is contained in our data? If noone's unloading lava nearby, temperature will change slowly over time, so every sample is representative of 30 minutes --> 3 hours.

Example 2: suppose we count the number of people at a restaurant once a day at the same hour, 6 times.

• Sampling duration: 5 days.

• Do we have 6 days' worth of "number of people present in restaurant" information? Hardly; the number of people can vary wildly depending on time of day and day of week. Large variance. Instead, we can say that each of our observations reasonably captures the number of people over 1 hour span - giving us 6 hours' worth data (non-contiguous).

So more generally, we can say that "duration" of a sequence in terms of information contained is $N\cdot \Delta t_e$, where $\Delta t_e = $ "effective time represented by each sample". It can be less than, or equal to, but not greater than $f_s^{-1}$, as that'd imply that a sample at $t=0.1$ "speaks for" a sample at $t=0.2$ more than that sample itself. So $f_s^{-1}$ is maximum represented duration.

Whatever the case, we associate a "representative time" to each individual observation, ultimately doing $\cdot N$ rather than $\cdot (N - 1)$.

---

... or not. We may have a scenario where it makes more sense to say samples represent only what's between them - in which case we're back to $(N-1)$. The point of this answer is more to illustrate what "depends on definition" can mean (but still that $\cdot N$ makes more sense for most purposes) - which hopefully is conveyed.

Answer 8

Discrete Fourier Transform says it's A!

I derived the closed form solution for DFT of a sine, which says that the correct continuous-time expression for

$$ x[n] = \cos(2\pi f_0 \mathbf{t}[n]), \\ \mathbf{t} = [0, 1, ..., N - 1] \cdot s,\ s = \text{sampling period} $$

is

$$ x(t) = \Pi\left(\frac{t - (T - s)/2}{T}\right) \cos(2\pi f_0 t) $$

where $T = Ns$ is the duration, and

$$ \Pi(t) = \begin{cases} 1,\ -1/2 \leq t \leq 1/2 \\ 0,\ \text{otherwise} \end{cases} $$

is a rectangular window, which in this case is

$$ \Pi\left(\frac{t - (T - s)/2}{T}\right) \begin{cases} 1,\ -s/2 \leq t \leq T - s/2 \\ 0,\ \text{otherwise} \end{cases} $$

It spans half a sampling interval to left of first sample, and half to right of last sample!

---

This concurs with my other answer. It is, however, not an absolute - other definitions can be more useful depending on context. But if we're interested in how the DFT "sees" the sampling of a continuous function, this is it.

Answer 9

It's $N/f_s$. Because consider what happens if it's $(N-1)/f_s$ instead; take a sequence $x$ of 6 samples, sampling once per second. Going by latter, defining "duration" as that between samples, we get

Now what is half the "duration" of $x$? Well, take half the sequence and measure the same:

Bad. If on the other hand we define duration as intervals midpointed by samples:

Good to go. This definition is also better grounded physically; suppose we wish to integrate. Doing so, we'd draw Riemann shapes (e.g. rectangles) in the discrete case, but regardless of shape, we'd have $N$ bins, so if finding e.g. average velocity, the physical interval spanned by integration would be $N/f_s$.

To be clear, this is largely a matter of definition, as a case can be made the other way; above's meant to show ways in which $N/f_s$ is more sensible.