How to take into account phase differences when doing Fourier Transform?

Question

I apologize if the title seems very vague, I don't really know how to put it a different way.

From what I understand, the Fourier transform is essentially just doing a dot product between multiple sine waves of different frequencies with the original signal. When the "chosen" sine wave has the same frequency as a component in the signal, it will be in phase and produce peaks. If the "chosen" wave isn't in the original signal, then it will either be cancelled by the original signal, or produce smaller peaks.

Let's say that there's a 100Hz sine wave component in a signal with a phase of $\frac{\pi}{2}$. If I were to take the dot product with a pure sine wave of 100Hz with no phase, it would appear as if two signals are present, one at 95Hz and one at 105Hz:

Is there a way to negate the effects of this? I was thinking of taking the maximum of pure cosine and sine wave in order to take into account phase differences, but I get much more noise around the frequency component:

Note: I'm not using any windowing function (Hanning, etc.) I can post my Python code if that will help.

EDIT: I tried using the formula as per Marcus' comment, and I'm getting weird results:

def do_fft(y, rate, f):
    N = len(y)
    summ = 0
for n in range(N):
    summ += y[n] * np.exp((0 - 1j) * 2 * np.pi * n * (f/rate))
return float(summ.real)
#return float(abs(summ))



def selective_fft(y, rate, frequencies):
    ar = []
    for f in frequencies:
        ar.append(do_fft(y, rate, f))
    return ar

"frequencies" is an array of frequencies that I want to "test" for.

EDIT: Here is how I'm doing the pseudo-fourier transform (originally):

t = np.linspace(0, 0.1, 4410)
ar = np.arange(0, 500, 1).reshape((-1,1)) #The frequencies to test
m = np.tile(ar, (1, t.shape[0])) #create matrix for frequencies
time_matrix = np.tile(t, (ar.shape[0], 1)) #create matrix for t vector
a = 100 #frequency components
b = 200
c = 300
y = np.sin(2 * np.pi * a * t + np.pi/2) + np.sin(2 * np.pi * b * t) + np.sin(2 * np.pi * c * t)
yc = y.copy() #copy signal
y = y.reshape((-1,1)).T #Add column and transpose to get one row and 4410 columns
y_stacked = np.tile(y, (ar.shape[0], 1)) #stack the function based on how many frequencies to test (500 from before)
sub = np.sin(2 * np.pi * np.multiply(time_matrix, m))
sub2 = np.cos(2 * np.pi * np.multiply(time_matrix, m)) #use cosine
dotted= np.abs(np.sum(np.multiply(y_stacked, sub), axis = 1).reshape((-1,1))) #basically the dot product
dotted2 = np.abs(np.sum(np.multiply(y_stacked, sub2), axis = 1).reshape((-1,1)))

Answer 1

This is what it looks to me what you're doing: you're preparing a signal with mixed frequencies, then you're making a sin/cos matrix of multiple sines which are to be multiplied with the test signal, and then you're using the absolute value of each sine and cosine multiplications and then average them. You then consider the variation of these averages the "FFT". If I didn't get this wrong, then you're not doing it the correct way.

What you're actually performing is you're calculating the $a_n$ and $b_n$ terms for the Fourier transform. Those represent the real and imaginary parts of the frequencies. What you're plotting is the variation of those terms as you sweep a frequency, but the FFT plot is the magnitude.

And your problem is an XY one: you're saying that you get phase errors due to the FFT, but you're not using an FFT, just something that resembles it. At this point I still don't what exactly you're after: to find a particular frequency in a test signal, or to perform an FFT? Because, as shown in the comments, there are no two peaks for multiplying $\sin(t)\cdot\sin(t+\phi)$.

So I'll consider that this is what you want: to find the spectrum of a single frequency from within a test signal of multiple sines, as its phase varies. This is just the basic of the lock-in amplifier/filter linked in the comments, and this is the math of it ($s(t)$ is a sum of sines, using unity amplitudes):

$$\begin{align} x(t)&=s(t)+\sin(2\pi ft+\phi)&=s(t)+\sin(2\pi\dfrac{t}{T}+\phi) \tag{1} \\ a&=\dfrac{1}{T}\int_0^T{x(t)\sin(2\pi\dfrac{t}{T})\mathrm{d}t}&=\dfrac{\cos(\phi)}{2} \tag{2}\\ b&=\dfrac{1}{T}\int_0^T{x(t)\cos(2\pi\dfrac{t}{T})\mathrm{d}t}&=\dfrac{\sin(\phi)}{2} \tag{3}\\ \end{align}$$

Since you want the peaks for the amplitude, both terms are multiplied by 2. If $x(t)$ has a different amplitude, it will be a constant that comes out of the integration and simply multiply the final result. The magnitude will be $\sqrt{a^2+b^2}$. As for the frequency of that particular peak, it will be given by the second term, $\cos(2t)$:

$$\sin(t)\sin(t+\phi)=\dfrac{\cos(\phi)}{2}-\dfrac{\cos(2t+\phi)}{2} \tag{4}$$

Whether you are perfoming the above steps, or an FFT, the plotted result should be the same. For example, in Octave, for a simple sine with displacement (*n just normalizes the magnitude for the plot):

n = 128;
N = 8192;
wt = 2*pi*[0:n-1]/32;
x = sin(wt + pi/6);
s = sin(wt);
c = cos(wt);
xs = x.*s;
xc = x.*c;
a = mean(xs).*ones(1, N/4);
b = mean(xc).*ones(1, N/4);
X = fft(x, N);
Xs = fft(xs, N);
comp = hypot(a, b)*n;
cosphi = cos(pi/6)/2*ones(1, N/4)*n;
plot(abs(X), "", abs(Xs), "", comp, "", comp/2, "", cosphi)

And the result shows:

• X, blue: the spectrum of the original signal, matching...
• comp, yellow: the magnitude calculated through the Fourier coefficients
• Xc, orange: formula (4), or the spectrum of the signal multiplied with a reference sine (s, resulting xs), matching...
• comp/2, purple: half the magnitude of X
• cosphi, green: the DC value of xs -- note that it's DC, not a frequency peak

---

Just in case it's not clear, since you have the real and imaginary parts of the Fourier coefficients, then you have the magnitude (as seen in the code) and the phase as $\mathrm{atan2}(b,a)$. To prove this, too, here is a different perspective:

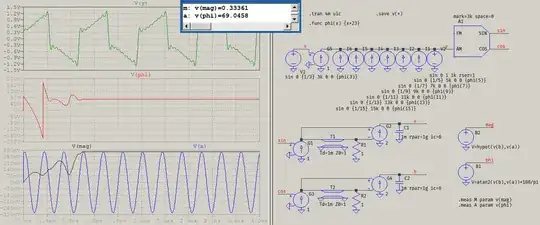
In the right pane, upper left, you see V(x) which is the frequency that's added to to the other ones. It's not the fundamental, 1 kHz, it's the first harmonic (3rd for only odd ones, 3 kHz). Its amplitude is ⅓ of the fundamental, and its angle is an odd multiple of the base angle which is seen at the top, in .func phi(x) {x*23}. It's the 3rd harmonic, thus it's three times that value. That FM/AM block multiplies the input signal, V(y) (plotted in green on the left), with unity sine and cosine of the desired frequency (3 kHz), averages them over one fundamental period (the whole bottom-left qurter of the schematic), giving the time quantities V(a) and V(b), representing the $a$ and $b$ coefficients. These, in turn, are used to generate the magnitude, V(mag) (black trace), matching the amplitude of the sine, V(x) (blue trace), and the angle, V(phi) (red trace). The magnitude and the angle are measured and their results are displayed in the small blue rectangle at the top (m for magnitude, a for angle). The results are not perfect because of roundings, waveform compression, no imposed timestep, etc, but the results are very representative of what I have been talking about so far: you don't need to have matching amplitudes in order to find the magnitude and the angle, since that is the whole purpose of the $a$ and $b$ coefficients. If this doesn't prove anything, I don't know what else to say, and you're better off waiting for someone else's answer.

---

Your comments give the impression that you haven't read anything that was said to you. Maybe you don't understand the math behind it (but then how come you said you read the article about the lock-in detection), or the code in Octave (though I kept it very simple, and quite close to what formulas you might see in books).

This is in Python. You used it in your OP, so you should be able to see what's going on. It follows the exact mathematical proof as above:

import numpy as np
t=np.linspace(0,2-1/500,1000)
phi=np.pi/18               # 10 deg
x=np.sin(2*np.pi*t+phi)    # fundamental
for i in range(2,10):      # add 10 harmonics of decreasing amplitude
                           # and increasing phase
  x=x+np.sin(2*np.pi*i*t+i*phi)/i
  i=i+1
n=3                        # check the 3rd harmonic, it should have
                           # 1/3 amplitude, 3*10 deg
s=np.sin(2*np.pi*n*t)      # reference sine, note the n*t
c=np.cos(2*np.pi*n*t)      # reference cosine
xs,xc=x*s,x*c
a,b=2*np.mean(xs),2*np.mean(xc)

At this point you have all you need. If the magnitude is not zero, the signal is there, and you can see what phase it has:

mag=np.hypot(b,a)
rad=np.atan2(b,a)
deg=rad*180/np.pi
mag,rad
(0.33333333333333326, 29.999999999999876)

As you can see, the amplitudes of the signals are not the same (reference sine is 1, 3rd harmonic is ⅓), yet the results are spot on. This means that the method works (not surprisingly).

At this point, the most basic of logic will tell you that, if this method gives the magnitude and the phase of a certain signal then a magnitude of zero will most certainly mean that there is no signal. Sure enough, since there are only 10 harmonics, searching for a 13th harmonic gives these:

s13=np.sin(2*np.pi*13*t)
c13=np.cos(2*np.pi*13*t)
xs13,xc13=x*s13,x*c13
a13,b13=2*np.mean(xs13),2*np.mean(xc13)
a13,b13
(4.369837824924616e-16, 7.993605777301127e-17)

Given your comments, I find it surprising that I have to insist in explaining, since you, yourself, said in the comments:

if that specific frequency doesn't exist, the signal will average out to zero over time

so then why do you ask how to tell if there is a signal when the magnitude is different than zero? Are you serious, or trolling? I hope it's not the latter, because it would mean you're mocking the time people dedicate, out of their own free time, to help others.