0

I would like to use Gardner loop to remove the timing offset in order to demodulate the signal. My signal contains the frequency offset, however I know that the Gardner loop can handle substantial frequency offsets and that is why I apply it.

I have written the following piece of code:

def Gardner_loop(time_support, sig):

sample_rate = 1/time_support[1]
sps = int(sample_rate/f_symb) # samples per symbol
sig_n_1 = int(np.ceil(sps/2)) # x(n-1)
sig_n_2 = int(sps) # x(n-2)   
loop_filter = f_symb//20 # BW of the loop filter
loop_num = 10000
error_symbol = np.zeros(loop_num)

error_list = []
sig_wo_time_err = []
step = 0


for i in range(1, loop_num):
    error_symbol[i] = sig.real[sig_n_1 + step + int(error_symbol[i-1]*loop_filter)]\
    *(sig.real[sig_n_2 + step + int(error_symbol[i-1]*loop_filter)]\
    - sig.real[step+int(error_symbol[i-1]*loop_filter)])\

    + sig.imag[sig_n_1 + step + int(error_symbol[i-1]*loop_filter)]\
    *(sig.imag[sig_n_2 + step + int(error_symbol[i-1]*loop_filter)]\
    - sig.imag[step+int(error_symbol[i-1]*loop_filter)]) 

    step+=sps
    error_list.append(error_symbol[i])

    # Update

    sig_wo_time_err.append(sig.real[sig_n_2+step+int(error_symbol[i-1]*loop_filter)] \
    + 1j*sig.imag[sig_n_2+step+int(error_symbol[i-1]*loop_filter)])

error_to_plot = np.array(error_symbol)
plt.plot(np.arange(1, loop_num+1), error_to_plot)
plt.xlabel('loop number')
plt.ylabel('error')
return np.array(sig_wo_time_err)

to remove timing offset. The BW of the loop filter I have selected from this article

In this case, sps = Number of samples per symbol = sampling frequency / symbol rate = 4.7. However, it seems to me that the loop is not locked since the error fluctuates as in the picture below:

non-interp

This is not interpolated signal.

My idea was to increase the number of samples per symbol to reduce the error and lock the loop. After interpolation, the number of samples per symbol = interpolated rate/symbol rate = 5. However, the error still remains and is depicted below:

interpolated

I have spent many hours trying to tackle on this problem, however I still do not understand what am I doing wrong. So my question is: do I make a mistake somewhere in the code, or do I miss something else to remove the timing offset?

Update:

I have updated the code where I save the signal.

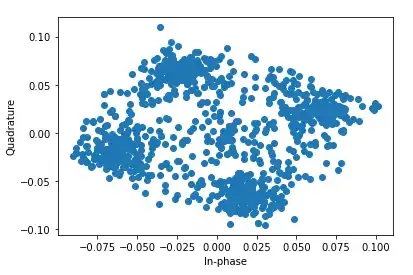
My constellation without interpolation for 1000 samples before timing recovery looks like this:

before symbol timing recovery

After symbol timing recovery, again for 1000 points (or for 1000 loops in the Gardner loop)

sig after gardner

For the same 1000 loops, my error is represented in the picture below

error

Note that if I plot more than 1000 samples, constellation becomes not readable anymore (which I think is due to the phase offset)

Python
  • 133
  • 6
  • 1
    The timing offset will never be zero. From your plots, it seems to be extremely small. What does the constellation look like? What is your BER? The timing offset error is not an end in itself. – MBaz May 17 '21 at 01:21
  • Right just as MBaz has said and to add what you may likely be seeing is the “self-noise” of the detector (which on a per sample basis is very noisy)- it is the long term average (as given by the loop BW that is of interest and the average of the plots show appears to be close to 0 which indicates things are working as expected (need to see for a much longer duration or test with an initial time offset to see that it does converge to zero, on average) – Dan Boschen May 17 '21 at 01:42
  • @MBaz thank you for the answer! I have updated the question and plotted the constellations before and after the timing recovery. BER - I do not know how to calculate yet. – Python May 17 '21 at 07:28
  • @DanBoschen thank you for the answer! I have updated the question with the constellations before and after the timing recovery. And also I have plotted an error over larger number of loops (1000 in this case) – Python May 17 '21 at 07:34
  • How many samples per symbol are you using? – Dan Boschen May 17 '21 at 12:05
  • @DanBoschen sps = int(4.7) = 5 – Python May 17 '21 at 12:13
  • I think you want to resample first such that you have a sample to choose that is (or would be with no timing error) exactly on the correct sampling location. With 4.7 you don't have that when you consider one sample to the next. I've used the Gardner successfully with 2 samples per symbol which provides the best timing SNR due to the position of the advanced and retarded sample and recommend doing that. – Dan Boschen May 17 '21 at 12:32
  • As Dan said, try resampling the signal so that you have two samples per symbol. Then, interpolate at the times calculated by Gardner. – MBaz May 17 '21 at 13:05
  • @MBaz I have the problems with the interpolation: do we need to interpolate inside the Gardner loop (and use the calculated instant for the further recovery) or we need to collect the error along the time support first and only then interpolate? – Python May 17 '21 at 19:16
  • @DanBoschen I would like to ask you one question: out of these 4.7 symbols, how do we select two the most appropriate for the Gardner loop? Or do we simply downsample the signal? – Python May 19 '21 at 20:10

0 Answers0