SNR should only be concerned within the spectrum of interest (Signal in Band to Noise in Band) as it is assumed that the rest can be filtered out(and that we would ultimately or could ultimately decimate down to Nyquist filtering out all upper frequency components in the process and provide reasonably sharp frequency selectivity at the lower sampling rate). For example, this is the reason we get an SNR advantage from oversampling: the quantization noise that is spread over the wider bandwidth is the same total quantization noise power, but we assume that we would of course filter out any of that noise not in band.
Once the spectrum for the band of frequencies is established, we will need either the signal with little to know noise, or the noise with little to no signal, in order to get any reasonable estimation of the SNR, or come up with some other isolation metric between signal and noise but using the spectrum won’t work without further information (such as any statistics or characteristics of the noise such can we asssume the noise will only be additive white Gaussian noise (AWGN)?. The horizontal axis as given by the OP is not clear what the frequency is (is this frequency or bin number?), but showing the spectrum in band specifically would help further to establish this.
Two approaches for measurement are to either capture the signal without the source present (if we don't have access to the clean source), or capture the signal right at the source if it can have a much higher SNR at that access point. With this the correlation coefficient can be used for accurate in-band SNR computation:
How can I find SNR, PEAQ, and ODG values by comparing two audios? '
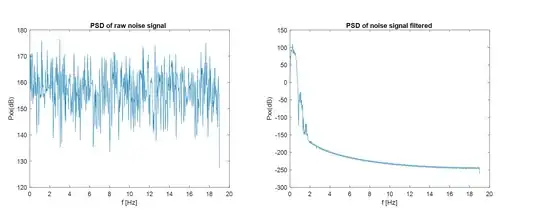
With a capture of noise alone, filter both captures to the band of interest and then compare the power in the two to get Signal + Noise compared to Noise. The ratio of the two would be S/N + 1.
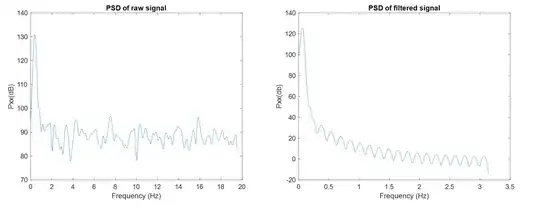
Below is an example of a spectrum where we could reasonably make an SNR estimation from the data directly to the extent we can assume that the same noise density that is out of band and can be separately measured and extends within the bandwidth of the signal with the same noise density, in this case we can filter the signal bandwidth alone to measure Signal + Noise and then filter the upper spectrum where only noise exists to measure the Noise. Converting this to a noise density (Noise Power /Hz) is easiest for this purpose. This is an example of an approach to do what is noted as required above with a single data capture; as we can establish some information about the noise that can be separately measured within the given spectrum.