Optimal idle or frame sync symbols for OQPSK

Question

Okay, everyone here knows that my thing was audio and that I have never gotten paid to do anything regarding communications systems. So, while I know a thing or two about DSP and even a little about discrete mathematics (from which we get GF2 or Maximum Length Sequences) I am very humble about my "expertise" in this area.

But OQPSK really intrigues me because it appears to me to be very elegant. (And people here know that I am in love with elegance in signal processing.) I have posted here a couple times. And once previously with a question and once over at the EE stack exchange.

Now, for the purpose of illustration, I am assuming we have a single bit stream, $a[n] \in \{$0,1$\}$, that becomes a bipolar bit stream

$$\begin{align} x[n] &\triangleq -1 + 2 a[n] \quad \in \{-1, 1 \} \\ &= -(-1)^{a[n]} \\ \end{align}$$

Now, part of what makes OQPSK so elegant is that the bits can be encoded onto bipolar quadrature signals $i[n]$ and $q[n]$ quite naturally where the even bits go into $i[n]$ and the odd bits go into $q[n]$. No delay is necessary, and no "dibit" symbols need to be formed as you would with non-offset QPSK.

$$\begin{align} i[n] \ &= \ g[n] x[n] \ + \ (1-g[n]) x[n-1] \\ q[n] \ &= \ (1-g[n]) x[n] \ + \ g[n] x[n-1] \\ \end{align}$$

where $g[n]$ is an even/odd gating signal defined as

$$ g[n] \triangleq \tfrac{1}{2}\left( 1 + (-1)^n \right) $$

and

$$ 1-g[n] = \tfrac{1}{2}\left( 1 - (-1)^n \right) $$

Note that for $n$ even, $g[n]=1$ and only $i[n]$ can change, while for $n$ odd, $1-g[n]=1$ and only $q[n]$ can change.

Now this is equivalent to having a rectangular pulse as the continuous-time symbol transmitted with each bit (assume the sampling period is the same as the bit period):

$$\begin{align} i(t) &= \sum\limits_{n=-\infty}^{\infty} x[2n] \, p(t-2n) \\ \\ q(t) &= \sum\limits_{n=-\infty}^{\infty} x[2n+1] \, p(t-(2n+1)) \\ \end{align}$$

where

$$ p(t) \triangleq \begin{cases} 0 \qquad & t < 0 \\ 1 \qquad & \qquad 0 \le t < 2 \\ 0 \qquad & \qquad \qquad \qquad 2 \le t \\ \end{cases} $$

But, if we're gonna contain the channel bandwidth, then a better symbol pulse is:

$$ p(t) = \operatorname{sinc}\left( \tfrac{t}{2} \right) w(t) $$

where

$$ \operatorname{sinc}(u) \triangleq \begin{cases} \frac{\sin(\pi u)}{\pi u} \qquad & u \ne 0 \\ 1 & u = 0 \\ \end{cases}$$

and $w(t)$ is a good window. It could be a Hamming window

$$ w(t) \triangleq \begin{cases} \tfrac{27}{50} + \tfrac{23}{50} \cos\left(2\pi \tfrac{t}{M}\right) \quad \quad & |t| \le \tfrac{M}{2} \\ 0 & |t| > \tfrac{M}{2} \\ \end{cases} $$

but, I still am a partisan for the Kaiser window in this application:

$$ w(t) \triangleq \begin{cases} \frac{1}{J_0(\beta)} J_0\left(\beta \sqrt{1 - \left(\frac{t}{M/2}\right)^2} \right) \quad \quad & |t| \le \tfrac{M}{2} \\ 0 & |t| > \tfrac{M}{2} \\ \end{cases} $$

$J_0(\cdot)$ is the 0th-order modified Bessel function of the first kind.

$$ J_0(u) = 1 \ + \ \sum\limits_{k=1}^{\infty} \frac{1}{(k!)^2} \left(-\frac{u^2}{4}\right)^{k} $$

$M+1$ is the number of non-zero samples or FIR taps. $\beta$ is a "shape parameter" and O&S recommend this heuristic:

$$ \beta = \begin{cases} 0.1102 \cdot (A-8.7) & A>50 \\ 0.5842 \cdot (A-21)^{2/5} + 0.07886 \cdot (A-21) \quad & 21 < A \le 50 \\ 0.0 & A \le 21 \\ \end{cases}$$

$$ M = 2 \left\lceil \frac{A-8}{4.57 \cdot \Delta\omega} \right\rceil $$

$A$ is the desired stopband attention in dB and $\Delta\omega$ is the desired width of the transition band in normalized angular frequency. $\lceil \cdot \rceil$ is the ceiling function (i.e. "round up").

Then this becomes:

$$\begin{align} i(t) &= \sum\limits_{n=\lfloor t/2-M/4 \rfloor}^{\lfloor t/2+M/4 \rfloor} x[2n] \, \operatorname{sinc}\left( \tfrac{t-2n}{2} \right) w(t-2n) \\ \\ q(t) &= \sum\limits_{n=\lfloor (t-1)/2-M/4 \rfloor}^{\lfloor (t-1)/2+M/4 \rfloor} x[2n+1] \, \operatorname{sinc}\left( \tfrac{t-(2n+1)}{2} \right) w(t-(2n+1)) \\ \end{align}$$

$\lfloor \cdot \rfloor$ is the floor() function (always round down).

This has no ISI for either $i(t)$ or $q(t)$ (assuming the receiver is properly time-aligned, which is why synchronization is salient) and it occupies the entire band but (if the window is good) very little energy outside of the band. I am conviced that this "Nyquist FDM" is the right way to do this.

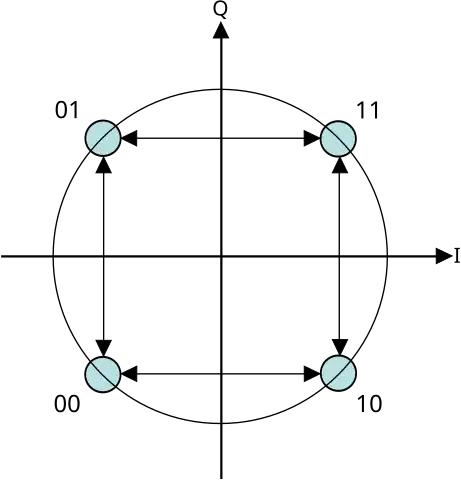
Now we can tell that any of these four sequences for $a[n]$ will not move the quadrature $i(t)\,+\,j\,q(t)$ vector around:

00000000000000000000000000000000

11111111111111111111111111111111

01010101010101010101010101010101

10101010101010101010101010101010

and that this sequence for $a[n]$ will send this quadrature vector spinning counter-clockwise at the maximum rotational speed:

00110011001100110011001100110011

and this in the maximum clockwise rotational speed:

01100110011001100110011001100110

Now I used to be saying that these would make good frame-sync symbols (and maybe idle channel signals) because they end up being two pure frequencies that are at the maximum and minimum frequencies in the band. I no longer think that is optimal because if the bands are packed like the Nyquist FDM (in the middle), I don't want heavy carriers hanging out at the bandedge possibly disturbing neighboring bands.

If the channel is idling, I now think it should be in the middle of the band rather than at the edge.

So now my question is, for an idle channel, what should be the bit pattern of the idle channel? One of those first four streams above (so that it is a constant position of the vector and rock-solid on the center frequency)? Or some other bit pattern that has just as many clockwise rotations as counter-clockwise rotations (so that the mean phase change is zero and the center frequency is zero and constant)? Should an idle channel occupy the Nyquist FDM bandwidth (nearly) completely? Or should it be only the center frequency.

And then my next question will be about Barker codes and using that for the "start bit" or the frame sync word.

Answer 1

If designing a new waveform and choosing parameters such as preambles, idle channels, etc, we need to be clear on what problems we are trying to solve, and these involve further details if known on the statistics of the data, the channel, and the type of demodulation. Typical receiver operations affected include channel estimation, frequency (carrier) recovery, timing recovery, and frame synchronization. This is balanced with the overhead that such features will add.

If the communications are for over the air channels that change with time, then any patterns that are sent other than data payloads are often those that allow for rapid synchronization in the receiver and good channel estimation to train equalizers. Any pattern that occupies a narrow frequency is a terrible choice for channel estimation: For channel estimation we want patterns that fill the spectrum that will be used as the equalization can only be done where there is energy to estimate the phase and magnitude at any particular frequency). This is one reason pseudo-random sequences make a good choice. For timing recovery a pattern with lots of bit transitions is best (such as 10101010101010 for a clock recovery loop). For frame synchronization a pattern that has an autocorrelation function that is maximum at tau=0 and zero everywhere else (white noise!) is best. Again the pseudo-random patterns approach this.

Same thing with the barker code such as my favorite to explain correlation with sequences so I know it by heart: 10110111000. That will add (in GF2) to 11 only when they are aligned and -1 everywhere else when we send that sequence repeatably. So this offers an alignment with processing gain on the aligned result ($10\log_{10}(11)$ dB increase in SNR when each sample is uncorrelated/independent) within that degree of granularity over the individual bit patterns. You'll see sequences in headers that are combinations of all of these features, combining PRN sequences with 101010101 patterns.