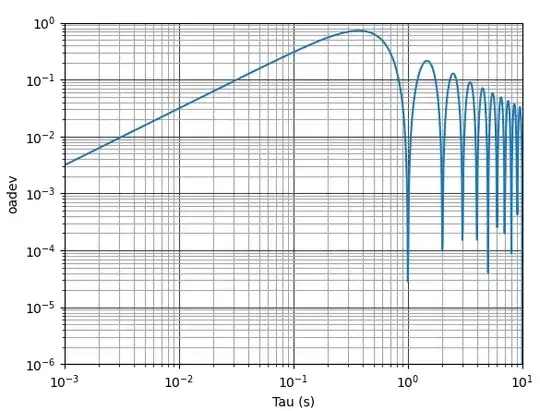
How to interpret ADEV plot?

Question

I want to understand how to interpret ADEV plots. I was of the understanding that if we see a peak at 1sec of TDEV plot there is a 1Hz noise in Time Interval Error(TIE) Capture.

To understand the relationship between TIE and TDEV I considered TIE to be a sinusoidal wave of 1Hz sampled using a signal of 20Hz (much greater than Nyquist requirement) and for a period of 10sec (tmax)

Sharing the code used:

import numpy as np
import allantools
from matplotlib import pyplot as plt
# import ipywidgets as widgets
from ipywidgets import interact, fixed
np.seterr(divide='ignore', invalid='ignore')
data generation
signal characteristics and sampling characteristics
freq = 1
tmin = 0
tmax = 10
sampling_period = 1/16
def generate_data(freq, tmin, tmax, sampling_period):
    t = np.arange(tmin,tmax,sampling_period)
    data = np.sin(2np.pit*freq)
    #data = 
    return data,t
def plot_data(ax, t, data):
    ax.plot(t,data)
def compute_adev(data, rate):
    # Load data
    a = allantools.Dataset(data=data,rate=rate,data_type="phase")
    # compute mdev
    a.compute('adev')
# Plot it using the Plot class
b = allantools.Plot()
b.plot(a, errorbars=True, grid=True)
# You can override defaults before &quot;show&quot; if needed
b.ax.set_xlabel(&quot;Tau (s)&quot;)
b.show()


def call_func(freq=1, tmin=0.0, tmax=10.0, sampling_period=1/20):
    data,t = generate_data(freq, tmin, tmax, sampling_period)
    ax=plt.axes()
    plot_data(ax,t,data)
    compute_adev(data, 1/sampling_period)
    call_func(1, 0.0, 10.0, 1/20)

The below Tdev Plot is using tmax=10.0

The below Tdev Plot is using tmax=100.0

Question:

The plot is not having peak at 1Hz. Since the input TIE is periodic over 1Hz, shouldn't we expect a peak at Tau = 1sec ?

PS. since i need 300points to create a tag, tagging time-freq and time-domain

It looks like you are plotting ADEV, not TDEV-- did you mean ADEV in your question? — Dan Boschen, Mar 17 '22 at 11:22

Dan Boschen · Accepted Answer · 2022-03-17T11:56:18.873

I explain the interpretation of ADEV plots in more detail at these posts.

How to interpret Allan Deviation plot for gyroscope?

Allan Variance vs Autocorrelation - Advantages

Is Allan variance still relevant?

Specific to the final question by the OP: The Allan Deviation will have a dip at the inverse of the period of an oscillation, not a peak. The peak occurs at approximately half the period (which is intuitive when you consider Allan Deviation is computed by a subtraction of averaged blocks).

Increase the number of samples in the computation, and you will see the tell tale ADEV of a sinusoidal modulation, which is given by an aliased Sinc function multiplied with a comb response as given by the difference of the (moving for overlap-ADEV or block otherwise) averaging (the Allan Deviation is the standard deviation of the frequency vs time after such processing), as I show in the plot below.

The plot below is for a sinusoidal frequency error at a rate of $f_m = 1$ Hz with a peak fractional frequency deviation of 1. I prefer "Overlap ADEV" since it converges to the same result with less error for a given number of samples. Note the first dip occurs at $\tau=1$ corresponding to the frequency $1/\tau= 1$ Hz. The peak occurs at approximately $\tau = 0.38/f_m$.

python code used:

import allantools
import numpy as np
nsamps = 2**16
fs = 1000
freq = 1
t = np.arange(2*16)/fs
signal = np.cos(2np.pi freq t)
a = allantools.Dataset(data=signal,
                       rate=fs,
                       data_type="freq", 
                       taus = np.logspace(-3, 1,1000))
a.compute('oadev')
b = allantools.Plot()
b.plot(a, errorbars=True, grid=True)
b.ax.axis([1e-3, 10, 1e-6, 1])

b.ax.set_xlabel("Tau (s)")
b.show()

How to interpret ADEV plot?

data generation

signal characteristics and sampling characteristics

1 Answers1

Linked