I preface this answer with that I know little about WVD and never worked with it, but do know time-frequency, and synchrosqueezing, which shares similarities. Part of my answer will be for SSQ.
Re: ChatGPT
The WVD is a time-frequency representation that provides a high degree of resolution in both time and frequency.
No, oversimplified
It is useful for analyzing signals that have non-stationary properties, such as chirps and transient signals. The WVD can also distinguish between closely spaced frequency components, and can also show the instantaneous frequency of a signal.
Yes
On the other hand, the STFT is a widely used method in signal processing, and is useful for analyzing signals that are stationary or have slow time-varying properties.
So is DFT, misses the point
It provides a high degree of frequency resolution, but its time resolution is limited.
Nonsense, the whole point is we can tune it
Unlike WVD, it is not able to distinguish between closely spaced frequency components,
No
and it does not show the instantaneous frequency of a signal to the degree in which WVD can.
Yes
The major disadvantage of the WVD is the computational cost. It has a computational complexity of O(N^2) which makes it impractical for large data sizes.
No
Re: dorian111
When increasing the sampling length to improve the frequency domain resolution, the time domain resolution will deteriorate.
I can't tell if this refers to WVD or STFT. For STFT or any localized time-frequency method, it's wrong - the sampling rate, not duration, affects time resolution. WVD appears to have a global temporal operator, so it may be true there.
For WVD, it is generally believed that it is not limited to the uncertainty principle and can achieve the maximum mathematical accuracy of frequency domain resolution.
No method completely escapes Heisenberg, but it's true we can achieve practically perfect localization for certain classes of signals.
The general conclusion is that the accuracy of WVD is much higher than that of STFT.
No. This isn't even true for synchrosqueezing, which significantly improves upon WVD. The worst case in SSQ vs STFT is close, I can't say SSQ is better, and certainly not "much better". But it is true that the best case for SSQ is far superior.
The disadvantage is that the frequency spectrum will appear pseudo-frequency when there are multiple frequency signals in the data.
Unsure what this means, WVD is time-frequency, there's no "frequency spectrum" in standard sense. It's true that introducing additional intrinsic modes worsens WVD, esp. with "quadratic interference" (that SSQ lacks).
Compared with STFT, the calculation cost is much higher, and the performance is the difference between O(N2log(N)) and O(kNlog(N)). When the STFT sliding length is taken as the minimum limit of 1, k=N, and the performance of WVD is the same.
Not necessarily. The compute burden depends on what we need WVD for, and whether we window. Of chief consideration is information, and how much we lose, which can be measured - and conversely, how much we gain by computing the full WVD as opposed to a part of it. The original MATLAB synchrosqueezing toolbox used n_fft=N, with logic that DFT is length N, and which most will agree is completely unnecessary.
Without windowing, I imagine WVD is like a fancified Hilbert transform and struggles with more than one component - see Figure 4.18 and below. Windowing, particularly with kernels which make WVD complex, enable tremendous optimization, similar to CWT. These optimizations are unrealized in most code... for now.
$$X(\tau,f)=\int_{-\infty}^\infty x(t)w(t-\tau)e^{-j2\pi f t}dt $$
This is a correct STFT formulation which is what most libraries implement, but I'd like to note that it's bad.
$$W_x(t,f)=\int_{-\infty}^{\infty}x(t+\frac\tau{2})x^{*}(t-\frac\tau{2})e^{-j2\pi f\tau}d\tau $$
From this formula, something sticks out: $x(... \pm \tau)$. This screams boundary effects - a major disadvantage compared to STFT.
Re: original question
Two major advantages of the spectrogram (abs(STFT)) over WVD, or at least SSQ, is stability, and sparsity. SSQ, as a feature, is quite brittle to noise (in some ways, yet also more robust in other ways, see related). Sparsity may come as a surprise, as SSQ claims that's its advantage over STFT - and it is - but the form of sparsity that matters a lot is subsampleability.
Note, hop_size is just the subsampling factor for STFT. We can hop in the spectrogram because there's high redundancy along time, and doing so loses little information. Not the case with SSQ, which generates rough and spiky time-frequency geometries - subsampling it a lot means losing a lot, and not subsampling likewise means keeping too many data points to be useful for machine learning, not because of data size, but correlated features prone to overfitting.
As I understand, WVD is more a measurement tool - it can be used to describe time-frequency characteristics of time-frequency kernels, e.g. wavelets. Though really I don't know where its applicability ends.
Lastly, third major advantage, STFT doesn't straight up invent signals:
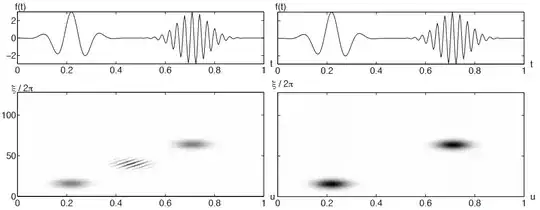
Figures 4.18 & 4.20, Wavelet Tour. Left is plain WVD, such interference is a dealbreaker for most applications. Right is windowed WVD, which attenuates interferences, but "reduces the time-frequency resolution" (under Eq 4.156).

