Is 2D circular cross-correlation with FFT done as described in this source?

Question

Given input images x and h of same size, greyscale 2D and potentially complex, we seek circular cross_correlate_2d(x, h) done with fft (so no padding) in image processing context.

I offer 1000 bounty to an answer that shows it's not exactly as described here. If it is exactly as described, then answers may state as such, but no bounty.

Bounty will be awarded to a differing cross_correlate_2d that passes below validation.

Answers that seek to argue against below validation by explaining how alternative definitions are more useful for general image processing are welcome. They are also subject to the bounty, but not guaranteed as it'll depend on whether I'm convinced.

Like checking any other source, this is a verification/clarification question.

---

Validation description

Following Cross-correlation Wikipedia on image processing, we seek similarity of x with h:

such that out[i, j] is strength of correlation of x with h being at i, j. Hence, if h = x, then peak will be at center of out, meaning the input aligns with itself when it fully overlaps itself, just as in full (padded) cross-correlation. Here's scipy, where I added imaginary WGN to an image:

The red circle is drawn around where(out == max(out)). More generally,

that's with a flipped false positive. With unflipped but conjugated, and real WGN:

Code to reproduce is available at Github.

Validation instruction

Change cross_correlate_2d below such that there's no AssertionError. No trickery, e.g. constant offset so technically it's different. It tests that above cases are reproduced, with images replaced by complex WGN.

def cross_correlate_2d(x, h):
    h = ifftshift(ifftshift(h, axes=0), axes=1)
    return ifft2(fft2(x) * np.conj(fft2(h)))
##############################################################################
import numpy as np
from numpy.fft import fft2, ifft2, ifftshift
def crand(s):
    return np.random.randn(s) + 1jnp.random.randn(s)
for M in (64, 65, 99):
    for N in (64, 65, 99):
        # case 1 -------------------------------------------------------------
        x = crand(M, N)
    o = cross_correlate_2d(x, x)
    hmax, wmax = np.where(abs(o) == abs(o).max())
    assert hmax == M//2, (hmax, M//2)
    assert wmax == N//2, (wmax, N//2)

    # case 2 -------------------------------------------------------------
    x = np.zeros((M, N), dtype='complex128')
    h = np.zeros((M, N), dtype='complex128')

    hctr, wctr = M//8, N//8
    hsize, wsize = hctr*2, wctr*2
    target_loc = slice(0, hsize), slice(0, wsize)
    false_positive_loc = slice(M//2, M//2 + hsize), slice(-wsize, None)
    target = crand(hsize, wsize)

    x[target_loc] = target
    x[false_positive_loc] = target[::-1, ::-1]
    h[M//2 - hctr:M//2 + hctr, N//2 - wctr:N//2 + wctr] = target

    o = cross_correlate_2d(x, h)
    hmax, wmax = np.where(abs(o) == abs(o).max())
    assert hmax == hctr, (hmax, hctr)
    assert wmax == wctr, (wmax, wctr)

    # case 3 -------------------------------------------------------------
    x[false_positive_loc] = np.conj(target)

    o = cross_correlate_2d(x, h)
    hmax, wmax = np.where(abs(o) == abs(o).max())
    assert hmax == hctr, (hmax, hctr)
    assert wmax == wctr, (wmax, wctr)

Answer 1

For the question's approach of shifting the h input image spatially using ifftshift before frequency-domain complex-conjugation, a possible motivation is to consider that the circular cross-correlation output is also an image, that the input images have anchors at their (non-periodic) centers, and that for identical input images, to indicate no displacement between the images, a peak of the circular cross-correlation output should appear at the anchor point of the reference input image h. Note that this answer assumes periodic input images, no padding, throughout, except for the notion of a non-periodic center of an image which is indirectly implied in the question.

Let's first have a look at what the question's shifting approach does in the even and odd period cases when the input images are identical impulses or impulse trains if considering the periodicity, compared to no ifftshift which would result in circular cross-correlation peaking at the first output sample. It suffices to look at the 1-dimensional case:

import numpy as np
from numpy.fft import fft, ifft, fftshift, ifftshift
x = [1, 0, 0, 0]
h = [1, 0, 0, 0]
print(np.real(ifft(fft(x) * np.conj(fft(ifftshift(h))))).astype(int))

[0 0 1 0]

That was a shift of N/2 for the even period N case, compared to [1 0 0 0].

x = [1, 0, 0, 0, 0]
h = [1, 0, 0, 0, 0]
print(np.real(ifft(fft(x) * np.conj(fft(ifftshift(h))))).astype(int))

[0 0 1 0 0]

That was a shift of (N - 1)/2 for the odd period N case, compared to [1 0 0 0 0].

Note that identical behavior would be obtained by removing the ifftshift and by fftshift of the circular cross-correlation output:

fftshift(ifft(fft(x) * np.conj(fft(h))))

It may be useful to look at the even and odd period cases in combination with 0-based and ½-based indexing schemes, both commonly used in image processing. Spoiler: It will turn out that the indexing scheme doesn't matter, so for simplicity you may wish to look at just the 0-based indexing scheme in the following:

The pixel indexes are shown as red dots, and the shared anchor index of the input images is shown as a cross. Now we test the question's proposed circular cross-correlation shifting scheme, on whether the peak of the circular cross-correlation output for identical inputs will be at the anchor index or not:

• With 0-based indexing and an even period 4 the output of the question's circular cross-correlation method peaks at index 2, which is unfortunately not at the anchor index 1.5. ❌
• With ½-based indexing and an even period 4 the output of the question's circular cross-correlation method peaks at index 2.5, which is unfortunately not at the anchor index 2. ❌
• With 0-based indexing and an odd period 5 the output of the question's circular cross-correlation method peaks at index 2, which is at the anchor location 2 as desired. ✅
• With ½-based indexing and an odd period 5 the output of the question's circular cross-correlation method peaks at index 2.5, which is at the anchor location 2.5 as desired. ✅

In summary, the question's approach of using ifftshift results in a small indexing error of half a sampling period, for the even period case. This problem cannot be solved by any non-interpolating shifting scheme. Cross-correlation of band-limited signals is identically bandlimited so complex exponential modulation in frequency domain could be used to do an interpolative shift assuming that the input images are band-limited horizontally and vertically below half the horizontal and vertical spatial sampling frequencies.

An alternative, and I would think the standard approach, is to do no shifting at all in the circular cross-correlation calculation, as in this answer. Then a peak at the first sample in the circular cross-correlation output is quite intuitively, it being at index zero, understood as indicating zero displacement between the input images. This is in agreement with the mathematical definition of circular cross-correlation for finite discrete functions:

$$(f \star g)[n]\ \triangleq \sum_{m=0}^{N-1} \overline{f[m]} g[(m+n)_{\text{mod}~N}]$$

As an extension, an anchor coordinate based correction to the calculated argmax of circular cross-correlation can be added if displaced anchor coordinates are needed. While also allowing non-centered anchors, this however doesn't enable as intuitive (albeit slightly erroneous) visualization of the full circular cross-correlation output as the question's approach.

Another motivation behind the question's approach may be to detect displacements using local methods that do not handle wraparound because they were designed for non-periodic data. The shift by the question's approach approximately symmetrically maximizes the amount of displacement that can be detected by such methods.

After reading the original poster's (OP's) answer, I understand that a motivation to do it as OP suggests may be to maintain compatibility when extending a library cross-correlation function to support circular padding in addition to any existing padding modes. There, if the existing implementation assumes a certain origin and support of the inputs (machine learning libraries typically provide convolutional neural network functionality with "centered" convolution kernels), it would be natural and of least surprise to a user to maintain those for the circular padding mode. Documenting this does not necessitate redefining what is meant, mathematically, by circular cross-correlation.

I can't think of any actual image processing application for circular cross-correlation with equal size x and h, other than acceleration of non-circular cross-correlation, which to me is ruled out by the question's statement "we seek circular cross_correlate_2d(x, h)".

Answer 2

OP's approach follows three basic premises:

1. Output at i, j corresponds to similarity of kernel with input, with kernel centered at i, j, so that the input and output axes are perfectly aligned, as would be the case in 1D continuous time with inputs centered at $t=0$.
2. Centering indexing conventions are followed. The "center" can either be at index 0, or its fftshift which is N//2. Usual image inputs are never centered at index 0, so N//2.
3. The images, as-is, are ground truth. Pixels are discrete, so there's no such thing as "fractional index".

As will be shown, all standard filtering follows these premises.

Summary

1. Only OP's approach yields valid images as outputs, for valid image inputs
2. Only OP's approach yields outputs that can be used as features for vast majority of cases: distance algorithms, edge detection, contour tracing, etc
3. Only OP's approach yields outputs subject to subsequent filtering, e.g. after nonlinearity
4. Only OP's approach has the property that shifting the target in the image will shift the peak in the output by the same amount, for all shifts
5. Only OP's approach can utilize DFT properties to yield commonly expected behavior, like time reversal
6. Only OP's approach is consistent with filtering in vast majority of other contexts, including basic spectral manipulation (e.g. lowpass), STFT and CWT, and all of machine learning.

The following disclaimer is specific to this network's regular users: if any of these points are disputed, I'll only reply in comments if the entire answer has been read first.

Minimal version

When doing usual cross-correlation with same output mode, do you input the left or right image?

Right is what non-OP's approaches do, with the conj(fft2(h)) variant being within 1-sample shift:

import numpy as np; from numpy.fft import fft2, ifft2, fftshift
import scipy.signal
x = np.random.randn(30, 30) + 1j*np.random.randn(30, 30)
h = np.random.randn(30, 30) + 1j*np.random.randn(30, 30)
xs = fftshift(fftshift(x, axes=0), axes=1)
assert np.allclose(ifft2(fft2(x) * fft2(np.conj(h[::-1, ::-1]))),
                   scipy.signal.correlate2d(xs, h, mode='same', boundary='circular'))

Standard filtering

1. Low-pass, high-pass, band-pass, and much of rudimentary spectral manipulations are mostly done with zero-phase filters, so that: (a) filtering doesn't shift/delay the signal, or misalign its spectral contents; (b) the filter isn't asymmetric so that left or right side of windowed input isn't favored. Zero-phase means real-valued in Fourier; this guarantees that the filter is centered at either 0 or N//2.

2. CWT, STFT, and all time-frequency analysis is done per premise 1.

3. Convolution and cross-correlation with 'same' output mode, which ensures that output size equals input size, unpad in a way that ensures premise 1, in every major implementation (NumPy, scipy, MATLAB, all of machine learning). The unpadding is done with surgical precision to ensure this: we unpad such that at each boundary edge, the kernel overlaps (is centered over) input as much as possible.

All of this follows an extremely basic objective of a time-to-time transform: alignment. Output at $t_0$ corresponds to input being modified around $t_0$. For an LTI system with impulse response $h$, the output at $t_0$ is a modification of input with $h$ centered over $x(t_0)$, such that $y(t)$ and $x(t)$ are directly comparable, and that if $h$ is the unit impulse, then $y(t) = x(t)$.

Standard filter formulation

In continuous time, virtually all filters will look like what's on the left rather than on the right:

It's done for same reason all of mathematics is done oriented around the origin, whenever it's the case: it's the reference coordinate. Even if we were to center elsewhere, where would it be for IIR filters? It'd be just as arbitrary as centering at $t=0$, and in the end we'd still have to align it with input to get what we want.

Yes, this is all very basic. And partly for same basic reasons, when we sample a time-domain filter in code, we get something that looks like this:

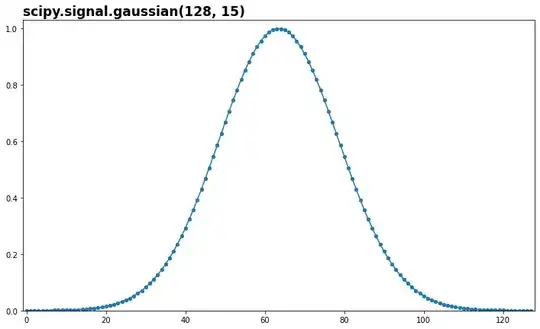
which is also what all major implementations will return windows as, and indeed this imports from scipy.signal.windows. Yet, they won't do filtering this way; all filtering is done zero-phase, 0-centered. For images, it means this MATLAB example would be:

Onto the premises:

P1: Input-output alignment

This agrees with the origin definition of cross-correlation:

$$ (x \star h)(\tau) = \int_{-\infty}^{\infty} x(t) \overline{h(t - \tau)} dt \tag{1} $$

Output at shift $\tau$ corresponds to the kernel, $h$, being shifted by $\tau$. Combined with the standard of centering $h$ over $t=0$, this becomes "$h$ being centered over $\tau$".

P2: Center index is either 0 or N//2

All major library-generated filters, if visually centered, will be centered with respect to N//2. Scipy example:

from scipy.signal.windows import hann
for N in range(64, 129):
    for sym in (True, False):
        w = hann(N, sym=sym)
        assert w[N//2] == w.max()

For sym=True, it also passes for N//2 - 1, since by definition it means left half of array equals right, and putting the second peak at N//2 + 1 would be farther off center. sym=False, the intended option for windowed FFT, only passes for N//2. ifftshift moves the peak to index 0.

More pertinently, we're working with FFT, which is centered about 0. fftshift moves this center to N//2, which is why ifftshift moves to 0. These conventions enforce DFT properties; if centers were anywhere else, we'd lose, for example, $x[n] = x[-n] \Leftrightarrow \text{zero phase}$, where negative indexing is circular per DFT's definition. Most properties would lose duality without intermediate and domain-specific shift manipulations. Conversely, if a time-domain manipulation doesn't follow said centering with standard FFT, it won't affect FFT as intended: flip(x) is not time-reversal.

P3: Discrete is ground-truth

Suppose this is false. Then every major library and centering conventions are invalidated.

Of course, we can insist on being centered over fractions, which would require bandlimited half-index-shift interpolation for the even case. This is a valid, yet completely separate sentiment, and completely separate operation that is regardless forced to build (operate) upon a non-fractional indexed output.

Other useful properties

OP's proposal is the only one that satisfies

$$ \tau + 1 > \tau $$

For ifft(fft(x) * conj(fft(h))), index N//2 and N//2 + 1 are apart by N//2: there's a jump-discontinuity, and indexing is no longer ordinal. This invalidates discrete-continuous domain correspondence, as continuous domains (in any signal processing) are by definition ordinal.

This discontinuity invalidates all spatially local operations upon the output. Any further filtering (e.g. after an intermediate operation), distance algorithms, edge detection, contour tracing - gone. OP's approach preserves spatial contiguity.

Re: Olli's answer

In summary, the question's approach of using ifftshift results in a small indexing error of half a sampling period, for the even period case. This problem cannot be solved by any non-interpolating shifting scheme.

i.e., if it's considered a problem, OP's approach suffers the same as the other alternatives in question.

Then a peak at the first sample in the circular cross-correlation output is quite intuitively, it being at index zero, understood as indicating zero displacement between the input images

Quite unintuitively, index N//2 - 1 is displacement by N//2 - 1, and index N//2 is displacement by -N//2. Shifting target in image by T left or right won't always shift output's peak by T left or right - likewise for up and down.

Another motivation behind the question's approach may be to detect displacements using local methods that do not handle wraparound because they were designed for non-periodic data.

In other words: if your inputs are valid images and you want a valid image output, use OP's approach. Indeed this refers to spatial contiguity.

Re: other approaches

We contrast OP's approach with others' by exploring latter explicitly. This section primarily concerns advocacy for fft(flip(conj(h)))-based approach with the goal of being exact, which was described in this answer by @Gillispie.

Following the answer's setup, Gillispie seeks to show that, in order to obtain equivalence between convolution and cross-correlation, we must time reverse correctly. Regardless of whether or not that point is achieved correctly, there's no mention of the critical practical fact that input images are visually centered, and that not accounting for it will run into all the problems described in this answer. Turns out, it's also not achieved correctly.

To be safe, we examine the relevant portions that show the objective is to be exact when it comes to circular time reversal:

The reason is that for discrete signals such as images, conjugation in the Fourier domain does not equate to time reversal. Rather, it performs modulo N time reversal: $ [x_1, x_2, x_3,... x_N] => [x_1, x_N, x_{N-1}, x_{N-2},... x_2]$.

This completely correct observation is, unfortunately, spinned into the opposite conclusion. We re-iterate the motivation of equivalence, also of correspondence between time and freq domains:

The conjugation property of the continuous time Fourier transform says that conjugating in the frequency domain conjugates and flips in the time domain: $\mathcal{F}^{-1} (\overline{X(\omega)}) = \overline{x(-t)}$ . So you should be able to perform cross-correlation via FFT by just conjugating one of the FFTed vectors, right? Wrong!

So the goal is $\mathcal{F}^{-1} (\overline{X(\omega)}) = \overline{x(-t)}$, in discrete. If readers were careful with this answer, they already see the problem. If not, let's be explicit: "$x(-t)$" assumes the existence of $x(0)$. Yet, $x(0)$ is not at index 0 - it is at index N//2, as Gillispie is aware by stating that flip is the solution. So, we seek $x[n] \rightarrow x[-n]$, with $x[0]$ at N//2. This is not achieved:

It's not achieved for any other choice of $x[0]$ centering either - not N//2 + 1, not N//2 - 1, not 0, or anything else. It is not achieved with Jdip's approach either. It is, ironically, achieved only with OP's approach:

A separate but related problem is described by Olli:

Gillispie is right to emphasize the concern, as it has numerous implications. For a zero-phase complex filter, for example, conjugation is identical to time reversal, but only if it's done right.

The motivation for OP's answer to the linked Q&A was two-fold: to correct Gillispie on his own goal, and to pose the most useful variant of cross-correlation for general image processing. After reading this answer of mine, let the reader judge whether OP succeeded.