Relationship between IDFT and discrete Fourier series?

Question

I want to know how IDFT

$$x_n = \frac{1}{N} \sum_{k=0}^{N-1} X_k\cdot e^{\frac{i 2 \pi}{N} k n}$$

is related to discrete Fourier series (Eq. 3)

$$x_{_N}(n) = \sum_{k=-N}^N C_k \cdot e^{\frac{i 2 \pi}{N} k n}$$

I might define $C_k=X_k/N$ but I am not sure why the latter uses different range of frequencies, including negative frequencies.

There are quite a few questions and answers about the relationship of the DFT to Discrete Fourier Series. They are essentially the same thing.. If the input to the DFT, $x[n]$, is real, then there is a Hermitian symmetry of the resulting $X[k]$ that makes the latter half the same as for negative frequencies. — robert bristow-johnson, Dec 15 '23 at 18:05

score 1 · Accepted Answer · answered Dec 15 '23 at 12:34

I think Wikipedia's notation using "partial sums" is somewhat confusing. From the page:

shown here as partial sums. But in theory $N \rightarrow \infty$

You are also misquoting it. The correct version should be

$$x_{_N}(t) = \sum_{k=-N}^N C_k \cdot e^{j2\pi\frac{k}{P}t}$$

Note that the divider in the exponent in the correct version is $P$ which is the period of the signal (a real number that's typically in units of time) and NOT $N$ which would be the length of the sum (a unitless integer).

A more common (and IMO more accurate) notation would be

$$x(t) = \sum_{k = -\infty}^{\infty} C_k \cdot e^{jk\omega_0 \cdot t}$$

where $\omega_0$ is the fundamental frequency, i.e. $\omega_0 = \frac{2\pi}{P}$

So the $N$ in both formulars are NOT the same N. In the IDFT N is the length of the DFT sequence, but for the Wikipedia version it's whatever the author uses as a definition for a "partial sum".

There are 4 flavors of the Fourier Transform depending and whether the signals are periodic/aperiodic and continuous/discrete. Periodicity in one domain results in the other domain being discrete, so the main difference in the flavors is that they use sums in the discrete domains and integrals in the continuous ones.

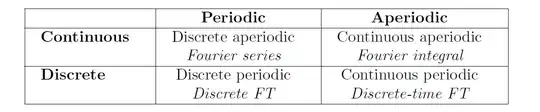
The naming is unfortunately a bit confusing but that's how it historically came to be.

Good reading for a deep dive into the 4 flavors and the exact relationships:

https://www.le.ac.uk/users/dsgp1/LODZLECT/Lodz5.pdf

That's where I lifted the table from.

Relationship between IDFT and discrete Fourier series?

1 Answers1