1

What's the minimum nearest neighbour approximation and upper approximation of this?

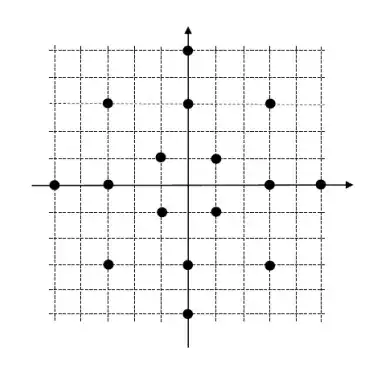
Consider a modulation design with the signal space diagram illustrated in the figure below. The signals are transmitted over an AWGN channel with power spectral density $ N_0/2 = 5 × 10^{−6}$. The maximum signal energy is $25 × 10^{−4}$. We assume that all the signals are equally probable.

enter image description here

suppose each grid has a length of d.

Nearest Neighbour approximation

The minimum distamce $d_{min} = 2d$

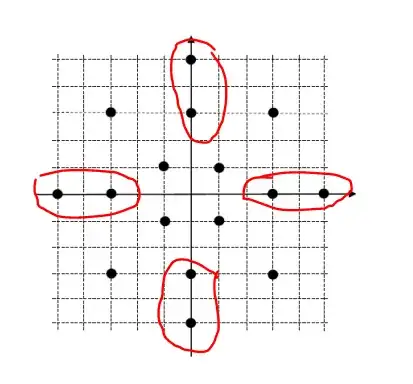
There are 8 of this pair who has only one nearest neighbor

enter image description here.

$$8 Q(\frac{2 d} {\sqrt{2 N_0}})$$

enter image description here

There are 4 points which has two minimum distance $2 d$.

$$8 Q(\frac{2 d} {\sqrt{2 N_0}})$$

$$P_e = \frac{1} {16} \biggl(8 \times 1 Q(\frac{2 d} {\sqrt{2 N_0}}) + 4 \times 2 Q(\frac{2 d} {\sqrt{2 N_0}}) \biggl)$$

Am I right? Can anyone give me a confirmation?

kile
  • 131
  • 3

1 Answers1

1

This isn't really my area, but I think your update missed out four points with a minimum distance of $2\sqrt{2} d$ in blue below:

Annotated signal constellation

So I think the original equation is better:

$$P_e = \frac{1} {16} \left(\color{red}{8 \times 1 Q\left(\frac{2 d} {\sqrt{2 N_0}}\right)} + \color{blue}{4 \times 1 Q\left(\frac{2 \sqrt{2} d} {\sqrt{2 N_0}}\right)} + \color{green}{4\times 2 Q\left(\frac{2 d}{\sqrt{2 N_0}}\right)} \right)$$

I'm going by this video.

Comparing the two, they do appear to be quite close.

Comparison

Code Only Below

No = logspace(-10,0,1000);
Pe1 = 1/16*(8*qfunc(2*d./sqrt(2*No)) + 8*qfunc(2*d./sqrt(2*No)))
Pe2 = 1/16*(8*qfunc(2*d./sqrt(2*No)) + 4*qfunc(2*sqrt(2)*d./sqrt(2*No)) + 8*qfunc(2*d./sqrt(2*No)))

plot(No, Pe1)
hold on;
plot(No, Pe2)
hold off;
Peter K.
  • 25,714
  • 9
  • 46
  • 91
  • since $d_{min} = 2d$, I don't think we should include those points who has distance greater than $2d$. – kile Dec 29 '23 at 22:32
  • @kile Understood! You might be right. As I said, not really my area. What I did might be the union bound, not the minimum nearest neighbor. – Peter K. Dec 29 '23 at 22:36
  • 2
    The usual, high-SNR approximation includes only those points at the constellation's minimum distance, sacrificing accuracy for simplicity. Including points at distances larger than $d_\text{min} = 2d$ makes the approximation a little bit more accurate, especially for lower SNR. In fact, including points at all distances makes the formula exact! – MBaz Dec 29 '23 at 22:57
  • 1
    The second nearest neighbors of the 4 corner points of the central (green) square are not the ones that you have used (inner ends of blue lines) but the inner ends of the red lines, which are at distance $\sqrt{5}d$ instead of $\sqrt{8}d$. – Dilip Sarwate Jan 29 '24 at 01:18