5

Lets say that we have a Standard Brownian Bridge ($\sigma=1$) with endpoints $(0,0),(1,0)$

Is there a way to derive the distribution of the area between a sample path of this bridge and the x-axis??

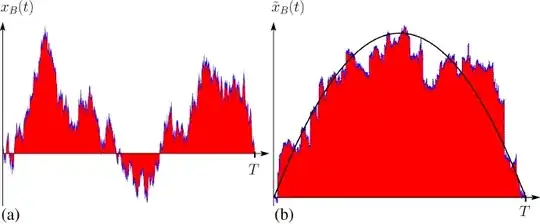
Below is an image that represents examples of my problem. I would want the distribution of the total area colored red in both examples:

enter image description here

Progress thus far

I've come up with crude bounds based on hitting time distributions, based on a formula for the distribution of the first time a standard ($\sigma=1$) Brownian bridge on $[0,T]$ with endpoints $(0,0),(T,x)$ hits level $b$. I found the formula here (see top of page 19).

$$P(\tau_b\leq T|T,x)=e^{\frac{-2b(b-x)}{T}}$$

In the interests of simplicity, I started my analysis to just the standard brownian bridge, where $T=1,x=0$, this simplifies the formula to:

$$P(\tau_b\leq 1)=e^{-2b^2}$$

Ok, now let $A$ be the area between a standard brownian bridge and the x-axis. I know that $P(A\leq a) \geq P\left( \{\tau_{c}>1\} \cap \{\tau_{c-a}>1\}\right),\; 0\leq c \leq a$, which is simply the probability that the brownian bridge is contained inside a rectangle of area $a$ on $[0,T]$ such that it contains the x-axis. The $\leq$ is justified since $\sigma(\{\tau_{c}>1\} \cap \{\tau_{c-a}>1\})\subset \sigma(\{A\leq a\})$.

Now, there is nothing special about any particular choice of $c$ in the above, so I'd like to integrate the RHS of above over all valid choices of $c$, for this, I need the density of $P\left( \{\tau_{c}>1\} \cap \{\tau_{c-a}>1\}\right)$ as a function of $c$.

$$P\left( \{\tau_{c}>1\} \cap \{\tau_{c-a}>1\}\right) = P(\tau_{c-a}>1)P(\tau_{c}>1|\tau_{c-a}>1)=\left(1-e^{-2(c-a)^2}\right)P(\tau_{c}>1|\tau_{c-a}>1)=\left(1-e^{-2(c-a)^2}\right)\left(1-P(\tau_{c}\leq 1|\tau_{c-a}> 1)\right)$$

The conditional probability measure $P(\tau_{c}\leq 1|\tau_{c-a}> 1)$ stops me from getting anywhere with this approach.

Question

Can the conditional measure $P(\tau_{c}>1|\tau_{c-a}>1)$ be derived? Is there another route to getting the distribution function of the area bounded by the standard brownian bridge?

  • 1
    @ Eurpraxis : Hi unless mistaken the (algebric) area between the Brownian Bridge $X_t$ and the x-axis is equal to $A_t=\int_0^t X_s ds$. A Brownian Bridge is a Gaussian process and so $A_t$ is itself a Gaussian random variable (think of it as the limit of Riemann sum of Gaussian random varaibles which is Gaussian). I would be very surprised if there was not results about this in the literature ( or even in lecture books on gaussain proceses) giving the first two moments of $A_t$. Best regards – TheBridge Nov 06 '14 at 15:10
  • @TheBridge thanks for taking interest in this question. I agree that the algebraic area will be gaussian ...its the variance that I have problems deriving due to the lack of independent increments. I have a partial solution that I am working on. Now, the geometric area (unsigned area in red) will not be gaussian, and it appears to be a very non-trivial problem. Any help in either would be appreciated. :) –  Nov 06 '14 at 16:13
  • In case someone is still interested in the question, a lot of information on this area (in particular integral formula density, recurrence relations for computing moments) and related quantities (area under Brownian motion, excursion, meanders) can be found with the appropriate pointers to the literature in Janson's survey referenced below. Janson, Svante, Brownian excursion area, Wright's constants in graph enumeration, and other Brownian areas, Probability Surveys, 4, (2007), 80-145 (electronic). DOI: 10.1214/07-PS104. – Valentin Féray Jan 06 '23 at 09:24

0 Answers0