The Taylor series (about $x=0$) for $\sin x$ is
$$
\sin x=\sum_{n=0}^\infty {(-1)^n x^{2n+1}\over (2n+1)!}.
$$
Here's what the sequence of partial sums (blue)
$$
S_N(x)=\sum_{n=0}^N {(-1)^n x^{2n+1}\over (2n+1)!}
$$
looks like as $N$ varies (here from $0$ to $12$) along with $y=\sin x$ (red):
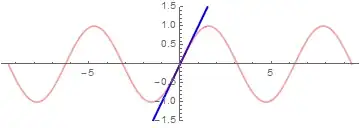
The idea is as we add more and more terms to the series, it gets closer and closer to $\sin x$ on a longer and longer interval (in this case since the interval of convergence is $(-\infty,\infty)$.)
Here's an example that has a finite interval of convergence to give you an idea what that entails. Using
$$
\sum_{n=0}^\infty x^n={1\over 1-x}, \quad -1<x<1,
$$
then substituting $-x^2$ in for $x$, we see
$$
\sum_{n=0}^\infty (-1)^nx^{2n}={1\over 1+x^2}, \quad -1<x<1.
$$
Here, the graph of $y={1\over 1+x^2}$ is shown in red and the $N$th partial sums of the series of various values of $N$ in blue.
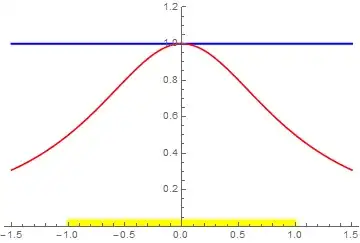
Note that as $N$ becomes larger, the blue graph matches the red graph closer and closer on the interval of convergence $-1<x<1$ (highlighted in yellow), but outside of that interval, it does not.
It might be helpful to read this and this which reinforce the idea of a Taylor series as an "infinitely long" Taylor polynomial. Once you are properly grounded in the motivation for and geometric interpretation of Taylor polynomials, you can carry those ideas over to (infinite) Taylor series.

