10

Given a sphere with radius r, a cone with radius r and height 2r, and a cylinder with radius r and height 2r, the sum of the volume of the cone and sphere is equal to the volume of the cylinder. If we look at the volume formulas, this is obvious. However, any ordinary person without mathematical training probably wouldn't find this intuitive.

I recall reading in a museum exhibit that before proving anything, Archimedes was able to slice up the sphere and cone and fit the pieces together into the cylinder--all in his mind. Can someone explain how one can slice up the shapes to do that?

pepsi
  • 489
  • 1
    Volumes of cones and cylinders depenc on more than just the radius, so I'm having trouble making sense out of your first sentence. – Gerry Myerson Feb 07 '12 at 04:47
  • 2
    http://www.cut-the-knot.org/pythagoras/Archimedes.shtml – JavaMan Feb 07 '12 at 04:50
  • @Gerry: I expect that the cone and cylinder have height equal to their base radius and to the radius of the sphere. – Brian M. Scott Feb 07 '12 at 04:53
  • 1
    @Gerry: I believe Archimedes worked under the assumption that $h = 2r$. – JavaMan Feb 07 '12 at 04:54
  • Would you happen to know Cavalieri's principle, by any chance? – J. M. ain't a mathematician Feb 07 '12 at 04:57
  • 1
    Very related. The difference is this question doesn't presume we know the volume of a cylinder. – anon Feb 07 '12 at 05:01
  • Thanks, pepsi, for adding the information about the heights. – Gerry Myerson Feb 07 '12 at 05:02
  • "This question has not received enough attention." pepsi, have you given any attention to the links supplied by Donezo and anon? Maybe instead of protesting that the question has not received enough attention, you could let us know what you find unsatisfactory about those links. – Gerry Myerson Jun 27 '12 at 00:57
  • @GerryMyerson 'This question has not received enough attention' are not my words--it was the option in the bounty form that fit best. I'm not protesting anything, merely trying to provide incentive for someone to answer the question. Neither of the links in the comments directly answered the question (which is probably why they were posted as comments). – pepsi Jun 27 '12 at 15:28
  • To answer your question, the link to Archimedes' notes appears to use center of mass to prove equal volume. The original question asks if/how it's possible to do it just by slicing pieces from the cylinder and combining them to form the others, or vice versa.

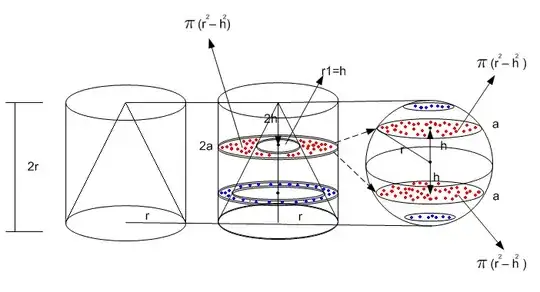
    The reference to Cavalieri's principle seems promising, but it still remains to be shown how the principle can be applied.

     – pepsi Jun 27 '12 at 15:28
  • 2
    This? – Ben Millwood Jun 27 '12 at 17:55

2 Answers2

7

I do not know how Archimedes did but I believe it was similiar way what I showed below. enter image description here

Mathlover
  • 10,058
1

Maybe this will explain things.

Gerry Myerson
  • 179,216