2

This is a follow-up to a question that I answered (though, not well enough).

Why is it that $\frac {\partial r}{\partial x} = \cos(\theta) = \frac {\partial x}{\partial r} = \frac {\partial}{\partial r}(r\cos(\theta))$?

$r$ and $x$ should be continuously differentiable so the inverse function theorem should apply. And I don't think $r$ should be a function of $\theta$ (even though $\frac {\partial r}{\partial x}$ is). Can someone explain this to me?

Community
  • 1
  • 1
    This all comes down to deciding what your independent / dependent variables are. If you are on a parametric curve given by $r=f(\theta)$, $r$ would depend on $\theta$, for instance. – Braindead Dec 13 '14 at 15:44
  • That's pretty much what I was thinking too. It would be nice if I could prove that $\dfrac {\partial x}{\partial r} = \sec(\theta)$, but without an explicit formula for $r=f(\theta)$ or $\theta=g(r)$, I don't know that it's possible. The best I can get is $\dfrac {\partial x}{\partial r} = \cos(\theta) -r\sin(\theta)\dfrac {\partial \theta}{\partial r}$. –  Dec 13 '14 at 15:47
  • If you are thinking about the mapping $(x,y)\to (r,\theta)$, then inverse function theorem does apply. You'll have to look at the Jacobian matrices. – Braindead Dec 13 '14 at 15:57
  • @Braindead My analysis of functions of several real variables is a little weak (I've been doing what amounts to linear algebra in Hilbert spaces and ODEs all semester), would you like to take a stab at answering this? –  Dec 13 '14 at 16:00

2 Answers2

2

Here is the right answer with prove.

Since you did the partial differentiation on the parametric equation, but it is not the only relationship between $x$ and $r$ in $r^2=x^2 + y^2$. The following section show you the right procedure:

$x^2 +y^2 =r^2$

$x^2 = r^2 - y^2$

$\frac{\partial (x^2)}{\partial {r}} = \frac{\partial( r^2 - y^2)}{\partial{r}}$

$\frac{\partial x}{\partial r} = \frac{r}{x} - \frac{y}{x}sin\theta$

$=\frac{1}{cos \theta} - \frac{sin^2 \theta}{cos \theta}$

$= cos \theta$

$\frac{\partial r^2}{\partial x} = 2x + \frac{\partial y^2}{\partial x}$

$\frac{\partial r}{\partial x} = \frac{x}{r} - \frac{y}{r} \frac{\partial y}{\partial x}$

$= \cos(\theta)-\frac{y}{r} \frac{\partial y}{\partial x}$

$=\cos(\theta)-\frac{y}{r}(\frac{r}{y} \frac{\partial r}{\partial x} - \frac{x}{y})$

$=\cos(\theta)-\frac{\partial r}{\partial x} +\frac{x}{r}$

$2\frac{\partial r}{\partial x} = 2\cos(\theta)$

The question here is why does $\frac{\partial x}{\partial r} = \frac{\partial r}{\partial x}$

For ease of understanding, I will show the surface $r^2 = x^2 + y^2$ and plot $| \sqrt{x^2+y^2}|$

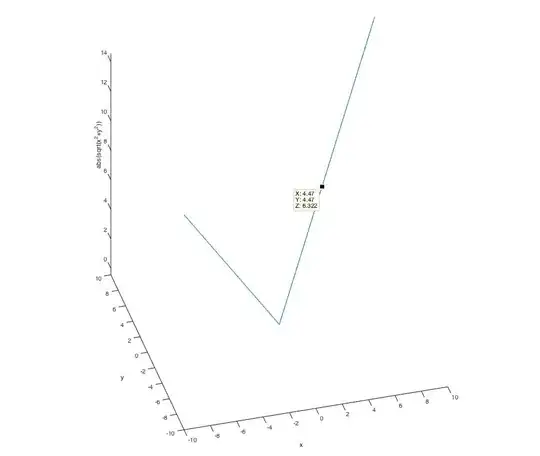
surface $r^2 = x^2 + y^2$ enter image description here $| \sqrt{x^2+y^2}|$

Our problem is $r^2=x^2+y^2$, with parametric equation $x=r\cos(\theta), y=r\sin(\theta), r>=0$.

Since we would like to know $\frac{\partial x}{\partial r}$, so turn the surface and look at the surface in direction which is parallel to y axis (figure 2), as a result, we only view the relationship between $x$ and $r$. Furthermore, the figure 3 shows the relationship between x, y and r.

From equation $r^2=x^2+y^2$, you can imagine that the from top view of the surface. The surface is composed by many circle with ascending radius, larger radius will at a higher level, result a clone. The relationship between r and x is x increase, radius increase. And the ratio is 1:1.

Therefore,

$\frac{\partial x}{\partial r} = \frac{\partial r}{\partial x} = \cos(\theta) = x/r = 1$

Lee Timothy
  • 83
1

Let $F: (x,y)\to (r,\theta)$ the usual change of coordinates.

The Jacobian matrix for $F$ (expressed in terms of $(r,\theta)$) is given by:

\begin{pmatrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta)/r & \cos(\theta)/r \end{pmatrix}

The Jacobian matrix for $F^{-1}$ is given by:

\begin{pmatrix} \cos(\theta) & -r\sin(\theta) \\ \sin(\theta) & r\cos(\theta) \end{pmatrix}

So IFT works.

Braindead
  • 4,999
  • Oh, right. That's how IFT works in higher dimensions. Thanks. –  Dec 13 '14 at 16:03
  • 1
    @Bye_World Be careful when working with partial derivatives of expressions that are not explicitly written as functions. If you are not paying attention to what are independent variables and what are dependent variables, you may end up doing a lot of symbolic manipulation that makes no real sense. – Braindead Dec 13 '14 at 16:08