Let's first write your equation as an imaginary part :
$$\tag{1}\Im\left((2\pi)^{iy}\,\sin\left(\frac {\pi}2\left(\frac 12+iy\right)\right)\Gamma\left(\frac 12-iy\right)\right)=0$$
For real values of $y$ the power of $2\pi$ and the $\sin$ won't provide zeros except the trivial $y=0$ (the $\sin$ function behaves nearly like $\sinh$ here) so that we will study only the zeros of $\;\Im\left(\Gamma\left(\frac 12+iy\right)\right)$ (which are also the zeros of $\;\Im\left(\Gamma\left(\frac 12-iy\right)\right)$ of course).
Let's start with an illustration of $\;\Im\left(\Gamma\left(x+iy\right)\right)\,$ to show our case $x=\frac 12$ in context :
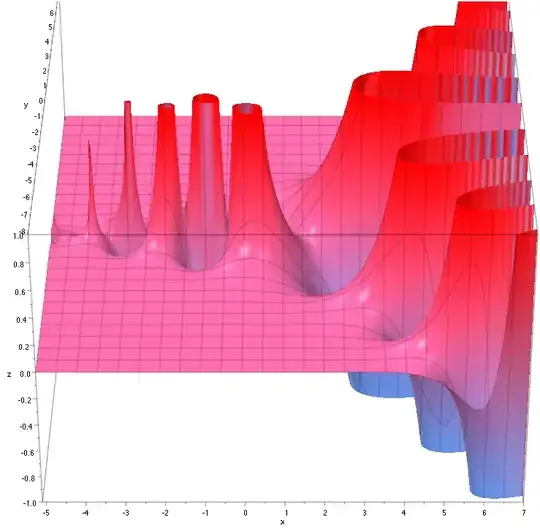
For other illustrations (including the real and absolute value parts) and interesting relations for $\Gamma$ in the complex plane see the thread "Real and imaginary part of Gamma function".
The relation $\left|\Gamma\left(\frac 12+iy\right)\right|=\sqrt{\dfrac{\pi}{\cosh(\pi\,y)}}\;$ found there allows us to 'rescale' the function so that the zeros become visible (else the oscillations would disappear quickly from the exponential decay far from $y=0$ as you may see in the previous picture).
Representation of $\;\Im\left(\Gamma\left(\dfrac 12+i\,y\right)\sqrt{\dfrac{\cosh\left(\pi\,y\right)}{\pi}}\right)$ :
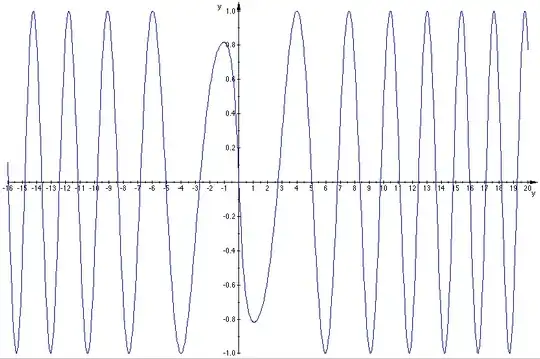
with the first non negative zeros approximately given by $y_k$ in :
\begin{array} {lll}
k&y_k&a_k\\
\hline
0&0&0\\
1&2.702691117402403870165565853&2.718281828\\
2&5.053344767849197367797351047&5.058444527\\
3&6.821889695106635313202928274&6.825074237\\
4&8.373032938914556281390088770&8.375376509\\
5&9.797707517468851913880784837&9.799572037\\
6&11.13617463421067206562439664&11.13772771\\
7&12.41062737183439804026853637&12.41196089\\
8&13.63490243932245059948493022&13.63607244\\
\end{array}
(of course the negative solutions are symmetrical and... you would have obtained the same solutions using Wolfram alpha !)
At this point let's notice that the imaginary part of $\Gamma\left(\dfrac 12+i\,y\right)$ will be zero iff $\Im\left(\log\,\Gamma\left(\dfrac 12+i\,y\right)\right)=k\pi,\quad \text{with}\;k\in\mathbb{Z}\;$ so let's use for example following asymptotic expansion of $\,\log\Gamma$ :
$$\tag{2}\log\,\Gamma\left(z\right)\sim \left(z-\frac 12\right)\log\left(z\right)-z+\frac 12\log(2\pi)+\sum_{n=1}^\infty \frac{B_{2n}}{2n\,(2n-1)z^{2n-1}}$$
$$\tag{3}\log\,\Gamma\left(\frac 12+i\,y\right)\sim \left(iy\right)\log\left(\frac 12+i\,y\right)-\frac 12-i\,y+\frac 12\log(2\pi)+\frac 1{12\left(\frac 12+iy\right)}$$
The imaginary part of this will be (after expansion for $y\gg 1$ and simplification) :
$$\tag{4}\Im\left(\log\,\Gamma\left(\frac 12+i\,y\right)\right)\sim y\,(\log(y)-1)+\frac 1{24\,y}$$
We want these values to be multiple of $\pi$ so let's try to revert the function of $y$ at the right (neglecting the $O(1/y)$ term) :
We may rewrite $\;f(y):=y\,(\log(y)-1)\;$ as $\;\dfrac{f(y)}e=\dfrac ye\log \dfrac ye\;$ and use the Lambert $W$ function's identity $\,W(x\log x)=\log x\;$ to deduce
$$\tag{5}\log \dfrac ye=W\left(\frac ye\log \frac ye\right)=W\left(\frac {f(y)}e\right)$$
that we will rewrite as $\;\displaystyle y=e^{\large{1+W(f(y)/e)}}\;$ so that the $k$-th zero $y_k$ (defined for $k>0$ by $\,f(y_k)=(k-1)\pi\,$ from the choice of the asymptotic formula for $\log\,\Gamma$) will be approximatively given by :
$$\tag{6}\boxed{\displaystyle y_k\approx a_k=\large{e^{\,1+W\left({(k-1)\,\pi}/e\right)}}},\quad\text{for}\;k\in\mathbb{N}^*$$
Concerning the zeros of $\zeta$ and their relations with the argument of $\zeta$ you may be interested by this thread.
ADDITION: To compare the zeros we obtained with these of the Riemann-Siegel $\theta$ function let's apply $(2)$ to $\;\displaystyle z=\frac 14+i\,\frac y2\,$ :
$$\tag{7}\log\,\Gamma\left(\frac 14+i\,\frac y2\right)\sim \left(\frac {iy}2-\frac 14\right)\log\left(\frac 14+\frac {iy}2\right)-\frac 14-\frac {iy}2+\frac {\log(2\pi)}2+\frac 1{3+6\,iy}$$
getting thus for $y\gg 1$ :
$$\tag{8}\Im\left(\log\,\Gamma\left(\frac 14+i\,\frac y2\right)\right)\sim \frac {y}2\,\left(\log\frac y2-1\right)-\frac {\pi}8+\frac 1{48\,y}$$
Subtracting $\;\log(\pi)\dfrac y2\;$ from the definition of $\theta$ we get
$$\tag{9}\theta(y)\sim \frac {y}2\,\left(\log\frac y{2\,\pi}-1\right)-\frac {\pi}8+\frac 1{48\,y}$$
so that, neglecting the $O(1/y)$ terms and solving $\theta(y)=(k-1)\,\pi$ (we may replace $k$ by $\frac k2$ as needed), we get $$k-1=\frac {\theta(y)}{\pi}= \frac {y}{2\,\pi}\,\log\frac y{2\,\pi\,e}-\frac 18$$ and
$\;\displaystyle \frac{k-\frac 78}e=\frac {y}{2\,\pi\,e}\,\log\frac y{2\,\pi\,e}\;$ that we will resolve as :
$$\log \dfrac y{2\,\pi\,e}=W\left(\frac y{2\,\pi\,e}\log \frac y{2\,\pi\,e}\right)=W\left(\frac{k-\frac 78}e\right)$$
obtaining thus this approximation of the Gram points :
$$\tag{10}\boxed{\displaystyle y_k\approx 2\,\pi\;e^{\large{1+W\left(\left(k-\frac 78\right)/e\right)}}},\quad\text{for}\;k\in\mathbb{N}^*$$
(a table of values is given in the link with a shift of one in the indice).

