From what I can gather from my old Graduate PDE course, what you want to do is use something called a Riemann function for the PDE. I refer to my text on the subject, Guenther & Lee, Partial Differential Equations of Mathematical Physics and Integral Equations, Prentice-Hall (1988), Sec. 4-6, pp. 114-121.
A Riemann function is akin to a Green's function for second-order ODE's and some PDE's. It is a mapping $R:\mathbb{R}^4 \to \mathbb{R}$, and is used as follows.
Consider the following integral:
$$\int_x^y dx' \, \int_{x'}^y dy' R(x,y,x',y') [u_{x'y'}(x',y')-u(x',y')] = 0$$
The integral is over a triangular region above the line $y'=x'$ and thus in the domain of the given PDE. Through a bit of trickery, we may rewrite the above integral equation as follows.
$$\int_x^y dx' \, \int_{x'}^y dy' [(R u_{x'})_{y'} - (R_{y'} u)_{x'} + (R_{x'y'}-R) u] = 0$$
We may try to solve this integral equation in many ways, but one way is to define $R$ so as to eliminate unknown quantities. For example, as we do not know $u$ in the integration region, we may require that
$$R_{x'y'}(x,y,x',y') - R(x,y,x',y')=0 \quad x \lt x', y \lt y'$$
We may also carry out the other integrations and form other requirements on $R$. I will summarize. When the following conditions are met:
$$R_{x'}(x,y,x',y) = 0 \quad x \lt x'$$
$$R_{y'}(x,y,x,y') = 0 \quad y \gt y'$$
$$R(x,y,x,y)=1$$
Then
$$u(x,y) = R(x,y,y,y) h(y) - \int_x^y dx' \, R(x,y,x',x') \phi(x') - \int_x^y dy' R_{y'}(x,y,y',y') h(y') $$
where $h(y)=u(y,y)$, $\psi(y) = u_y(y,y)$, and $\phi(y) = h'(x)-\psi(x)$. The equation defining $\phi$ is a result of a consistency condition:
$$h'(x) = \phi(x)+\psi(x)$$
Recall we are given $h(x) = x^2 \theta(x)$ and $\psi(x)=0$, $\theta$ being the Heaviside step function. NB $h'(x) = 2 x \theta(x) + x^2 \delta(x)$.
I refer you to the cited text as to determining $R$ given the above conditions. The result is
$$R(x,y,x',y') = J_0{\left ( 2 \sqrt{(x'-x)(y-y')} \right )} $$
$$R_{y'}(x,y,y',y')= -\frac{J_1{\left ( 2 \sqrt{(y'-x)(y-y')} \right )}}{\sqrt{(y'-x)(y-y')}} (x+y-2 y')$$
where $J_0$ and $J_1$ are the Bessel functions of the first kind, zeroth and first order respectively. The solution is then
$$\begin{align}u(x,y) &= x^2 \,\theta(x) + \int_x^y dy' \frac{J_1{\left ( 2 \sqrt{(y'-x)(y-y')} \right )}}{\sqrt{(y'-x)(y-y')}} (x+y-2 y') y'^2 \, \theta(y')\end{align}$$
ADDENDUM
Here's a plot of $u(x,x+k)$ for $k \in \{0,1,2,\ldots,9\}$:
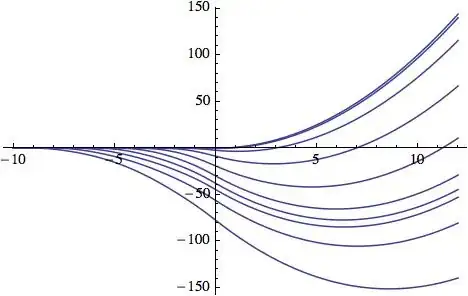

sol[x_, y_] := x^2 HeavisideTheta[x] + NIntegrate[(BesselJ[1, 2 Sqrt[(y - u) (-x + u)]] (x + y - 2 u))/ Sqrt[(y - u) (-x + u)] u^2 HeavisideTheta[u], {u, x, y}];
Plot[Table[sol[x, x + k], {k, 0, 9}], {x, -10, 12}]
I wouldn't use Plot3D because it would be hard to appreciate the behavior of the solution. For a start, I like plotting the curves as I have. You may want to rewrite the integral in terms of $u(x,x+k)$. ContourPlot is another option.
– Ron Gordon Dec 23 '14 at 00:39