A man who lies a fourth of the time throws a die and says it is a six. What is the probability it is actually a six?

Question

First, I apologise for the vague title. I couldn't think of a short way to represent the problem. Also, I am aware that a similar question exists, but I have a little bit more insight.

The problem is:

A man is known to speak the truth three out of four times. He throws a die and reports that it is a six. Find the probability that it actually is a six.

The answer in the book is $ \frac{3}{8} $, which sounds completely off to me, given the numbers, on first glance. I decided to try it on my own. After some contemplation, it indeed is true that $ \frac{3}{8} $ is correct. But, the question's vagueness makes it interesting. It's sort of a naive answer!

First, here's the book's solution:

Let $ E $ be the event that the man reports that a six occurs, $ S_1 $ be the event that six occurs and $ S_2 $ be the event that six does not occur.

$ P(S_1) $ = Probability that six occurs = $ \frac{1}{6} $

$ P(S_2) $ = Probability that six does not occur = $ \frac{5}{6} $

$ P(E~|S_1) $ = Probability that the man reports that a six occurred when it has actually occurred (truth) = $ \frac{3}{4} $

$ P(E~|S_2) $ = Probability that the man reports that a six occurred when it hasn't actually occurred = $ \frac{1}{4} $

$ P(S_1|E) $ = Probability that a six has actually occurred when the man claims so =

$$ \frac{P(S_1)~P(E~|S1)}{P(S_1)~P(E~|S_1)+P(S_2)~P(E~|S_2)} = \frac{3}{8} $$

Link to original: Page 25 of this (link updated 22/11/2015; tends to break often).

Here's the first of my two solutions:

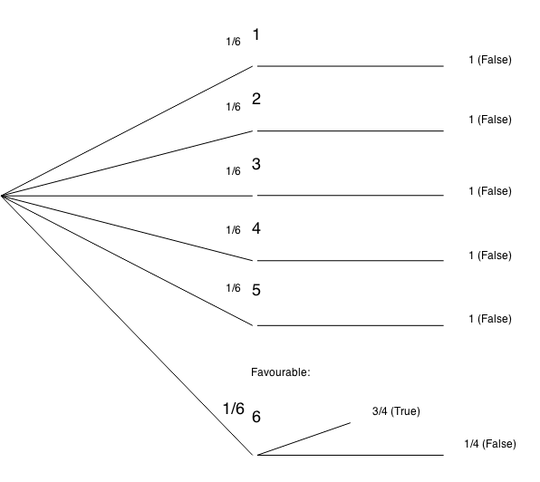
The question is a little vague and it doesn't tell us what the man says when he doesn't get a six. Assuming he lies every time he doesn't get a six (which is not quite what the question says), would bring up $ P(E~|S_2) $ to $ 1 $, which skyrockets $ P(lie) $ to $ \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6}.\frac{1}{4} = \frac{7}{8} $.

Also, $ P(E~|S_1) = \frac{3}{4} $ and $ P(E) = \frac{5}{6} + \frac{1}{6}.\frac{3}{4} = \frac{23}{24} $.

This brings us to, $$ P(S_1|E) = \frac{P(S_1)P(E~|S_1)}{P(E)} = \frac{3}{23} = 13.04\% $$

Please note that I don't care about the sixes rolled when he lies about it being a six, because that condition is not applicable to the question.

I'm very skeptical about my calculations! I decided to whip up a simple program and see what the probability distribution is for $$ \frac{Number~of~sixes~rolled~while ~saying~it's~a~six}{Number~of~dice~rolls} $$

Here's the result:

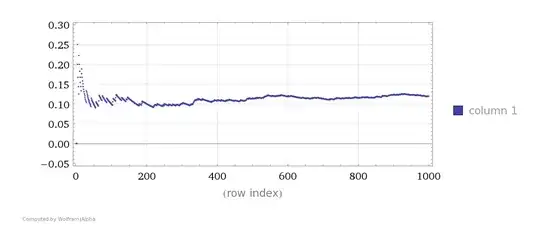
Considering the book says $ P(E~|S_2) = \frac{1}{4} $, which is in essence is contradictory to the question, let's also consider the other possibility:

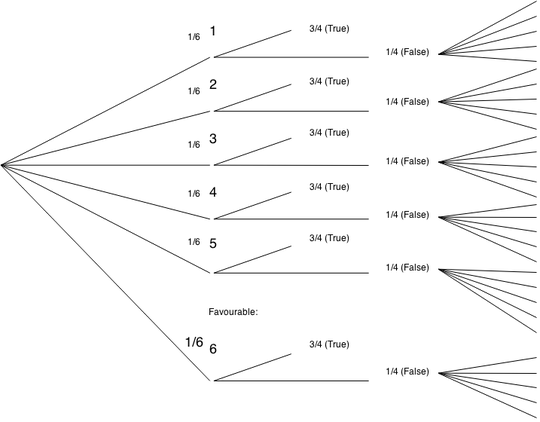
It's even more vague in this scenario! If the man lies after any given roll, there is a $ \frac{1}{5} $ probability that he will lie about it being any other number. This creates a new branch at each lie, which splits into five. In this case,

$$ P(E) = \frac{1}{6}.\frac{1}{4}.\frac{1}{5}.\frac{5}{1}+\frac{1}{6}.\frac{3}{4} = \frac{1}{6} $$

$ P(E~|S_1) $ still remains $ \frac{3}{4} $, but $ P(E~|S_2) = \frac{1}{4}.\frac{1}{5} = \frac{1}{20} $.

$$ P(S_1|E) = \frac{P(S_1)P(E~|S_1)}{P(E)} = \frac{3}{4} = 75\% $$

This seems like the more intuitive answer, and it is why I doubted the original answer in the first place. Given a truth probability of $ \frac{3}{4} $, there was no way that the probability of a six was $ 37.5\% $!

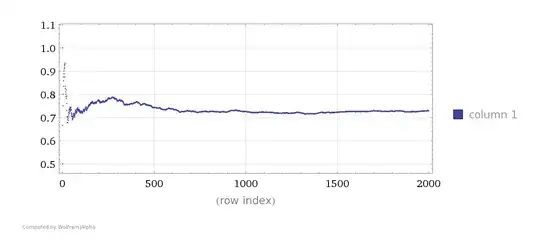
The ambiguity of the question is what makes $ \frac{3}{8} $ wrong to me. Entirely out of curiosity, which answer fits best with the question and are these calculations correct or baloney?

Answer 1

There are essentially three aspects of the question that I would consider vague:

1. The probability distribution of the outcome of the die roll is not explicitly stated--so in particular, are we to assume that it is a fair die?

2. Whether the event that the man lies about the die roll is independent of the true outcome of the die roll is not stated, and the official solution assumes that these events (the roll of the die, and whether the man lies or tells the truth) are independent.

3. If a six is not rolled and the man lies about the outcome, does the man lie in the sense of choosing any one of the other five numbers available to him, or does he lie in the sense of "I didn't roll a six but I will say I did?"

Item 3 is the real sticking point, since without making the assumptions of Items 1 and 2, no computation can be performed at all. But Item 3 requires us to interpret the meaning of "lie," and more problematically, a fully reasonable computation is possible under a variety of interpretations. To see why, let's make the process a bit more concrete:

1. The man rolls the die and observes the number rolled, which is hidden from you.
2. The man then flips a fair coin twice and again this outcome is hidden from you. If he gets two heads, he decides to lie; otherwise, he tells the truth.
3. If telling the truth, he reports the actual value of the die roll he observed.

Now consider two plausible interpretations of what happens if the man lies:

• (Option A) If he lies, then the value he reports is any value randomly and uniformly chosen from the remaining five possibilities.
• (Option B) If the actual value was a six and he got two heads, then he lies by choosing any other number from $\{1,2,3,4,5\}$; if the actual value was not a six and he got two heads, then he reports $6$.

It is under the interpretation of Option B that the "official" answer is $3/8$. But what about Option A? Let's do the computation. Let $X = 1$ if the true value of the die is six, and $X = 0$ otherwise. Let $Y = 1$ if the reported value of the die is six, and $Y = 0$ otherwise. Let $L = 1$ if the man lies, and $L = 0$ otherwise. Then we know $\Pr[X = 1] = \frac{1}{6}$, $\Pr[L = 1] = \frac{1}{4}$. We also know $$\Pr[Y = 1 \mid X = 1] = \Pr[L = 0] = \frac{3}{4},$$ and $$\Pr[Y = 1 \mid X = 0] = \Pr[Y = 1 \mid (X = 0 \cap L = 1)]\Pr[L = 1] = \frac{1}{5} \cdot \frac{1}{4} = \frac{1}{20},$$ because two things must happen for the man to report a six if no six was rolled: he has to flip two heads (and thus be allowed to lie) with probability $\frac{1}{4}$, and he must randomly and uniformly choose to report six with probability $\frac{1}{5}$. From this, we can now compute $$\begin{align*} \Pr[X = 1 \mid Y = 1] &= \frac{\Pr[Y = 1 \mid X = 1] \Pr[X = 1]}{\Pr[Y = 1]} \\ &= \frac{\Pr[Y = 1 \mid X = 1]\Pr[X = 1]}{\Pr[Y = 1 \mid X = 1]\Pr[X = 1] + \Pr[Y = 1 \mid X = 0]\Pr[X = 0]} \\ &= \frac{\frac{3}{4} \cdot \frac{1}{6}}{\frac{3}{4} \cdot \frac{1}{6} + \frac{1}{20} \cdot \frac{5}{6}} \\ &= \frac{3}{4}. \end{align*}$$ Therefore, the question lacks a critically important clarification: when the man "lies," is the nature of that lie of the form "I rolled a six (but I really did not) / I did not roll a six (but I really did)" (this is Option B), or is it "I rolled a one (but I really did not) / I rolled a two (but I really did not) / etc." (this is Option A)? Which option you choose affects the resulting probability calculation, and you can simulate either scenario to that effect.

Indeed, there are any number of possible interpretations, because ultimately what influences the desired conditional probability is the probability that the man will choose to report a six given that he has decided to lie after not actually rolling a six, and this is not specified in the question. Both options already described yield reasonable interpretations, but we could also recognize them as special cases of the general probability $$\Pr[X = 1 \mid Y = 1] = \frac{3}{3+5p},$$ where $p = \Pr[Y = 1 \mid (X = 0 \cap L = 1)]$. Option A sets $p = 1/5$ (choose uniformly among the other options), and Option B sets $p = 1$ (always choose to report 6).

Consequently, I would regard this question as having insufficient information to formulate a conclusive answer.

Answer 2

There are two situations in which the man can report a 6, either he is telling the truth or he is lying. The key assumption that seems to be made here is that the man's veracity is independant of the value on the die. Namely, he is just as likely to lie if the die shows a six as if it shows a three.

That being said, as you posted above, this is an example of Bayes Theorem. Let me change your nomenclature a bit.

Let $S$ be the probability of rolling a six $=\frac{1}{6}$

Let $\bar{S}$ be the probability of not rolling a six $=\frac{5}{6}$

Let $T$ be the probability of the man telling the truth, regardless of situation $=\frac{3}{4}$

Let $\bar{T}$ be the probability of the man not telling the truth, regardless of situation $=\frac{1}{4}$

Let $M$ be the probability the man says there was a 6. So what we want is: $$ P(S|M) = \frac{P(S \cap M)}{P(M)} $$

We don't immediately know $M$, true. What we do know is that $M$ comprises two situations: truth and falsity. In other words: $$ P(M) = P(T \cap S) + P(\bar{T} \cap \bar{S}) $$.

We are also luckily working under the assumption that the man's prevarication is independant of the die, so we can calulate $P(M)$ directly from the known $P(S)$ and $P(T)$. $P(S \cap M)$ is the case where the man tells the truth about the rolled six, which is $\frac{3}{4}\cdot\frac{1}{6}$. $P(\bar{S} \cap \bar{M})$ is the case where the man lies about anything other than a rolled six, which is $\frac{1}{4}\cdot\frac{5}{6}$. So the conditional probability of the there being a six, given that the man told us so, is the probability of the true case over the probability of all possible cases where the man says 6: $$ \begin{align} P(S|M) &= \frac{P(S \cap M)}{P(M)}\\ &= \frac{\frac{3}{4}\cdot\frac{1}{6}}{\frac{3}{4}\cdot\frac{1}{6} + \frac{1}{4}\cdot\frac{5}{6}}\\ &=\frac{\frac{3}{24}}{\frac{3 + 5}{24}}\\ &=\frac{3}{8} \end{align} $$