Double integral $ \iint \limits_D \frac{y}{x^2+(y+1)^2}dxdy$, $D$=$\{(x,y): x^2+y^2 \le1 , y\ge0\}$

Question

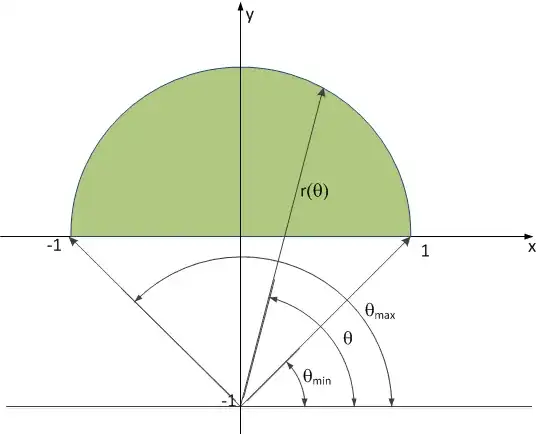
Solve $$ \iint \limits_D \frac{y}{x^2+(y+1)^2}dxdy \ \ \ \ . . . \ (*)$$

where $D$=$\{$$(x,y): x^2+y^2 \le1 , y\ge0 $$\}$

$$ $$ Here is my attempt.

$$\begin{align} &(1).\ \ \ (*)=\int_{-1}^1 \int_{0}^{\sqrt{1-x^2}}\frac{y}{x^2+(y+1)^2}dydx \\ &(2).\ \ \ (*)= \int_{0}^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}\frac{y}{x^2+(y+1)^2}dxdy \\ &(3). \ \ \int\frac{y+1}{x^2+(y+1)^2}dx = \arctan\left(\frac{x}{y+1}\right) + C \\ &(4). \ \ \ (*)=\int_{0}^{\pi} \int_{0}^{1}\frac{r^2sin\theta}{r^2+2rsin\theta+1}drd\theta \\\\ \end{align}$$

I used $(1)$, $(4)$ and $(2)$ with $(3)$,

but didn't solve yet. $$$$ Did I make a mistake?

Could you give me some advice, please?

How can I solve this integral...

Thank you for your attention to this matter.

$$$$ P.S.

Here is result of wolframalpha

$$$$

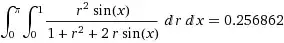
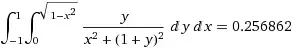
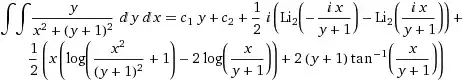
$$ $$ Additionally... I did like this.. maybe useless :-(

$$\begin{align} (*) & = \int_{0}^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}\frac{y}{x^2+(y+1)^2}dxdy \\\\ &=\int_{0}^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}\frac{y+1}{x^2+(y+1)^2}dxdy + \int_{0}^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}\frac{1}{x^2+(y+1)^2}dxdy \\\\ &=\int_{0}^1 \left(\arctan\left(\frac{\sqrt{1-y^2}}{y+1}\right) - \arctan\left(\frac{-\sqrt{1-y^2}}{y+1}\right)\right)dy \\ & \ \ \ \ + \int_{0}^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}\frac{1}{x^2+(y+1)^2}dxdy \\\\ &=\int_{0}^1 \left(\arctan\left(\sqrt\frac{1-y}{1+y} \ \right) - \arctan\left(-\sqrt\frac{1-y}{1+y} \ \right)\right)dy \\ & \ \ \ \ +\int_{0}^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}\frac{1}{x^2+(y+1)^2}dxdy \\\\ &= terrible?! \\ \end{align}$$

$$ $$

$$ $$ ---------------------------------------------------------------------------

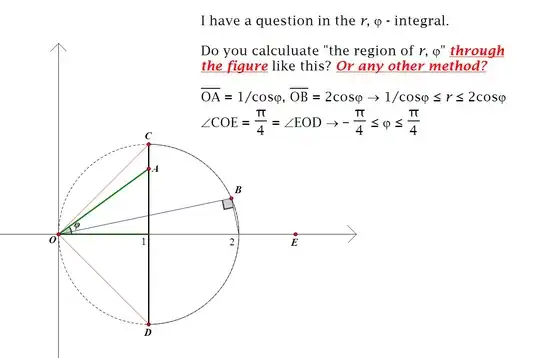
This picture is for asking to Christian Blatter

(I am really sorry, if I bother you guys for this picture.)

Answer 1

I shall introduce new coordinates (again denoted by $x$, $y$) such that the point $(0,-1)$ becomes the origin, and your vertical axis is my horizontal axis. Your integral then appears as $$J:=\int_H{x-1\over x^2+y^2}\>{\rm d}(x,y)\ ,$$ where $H$ is the right half of the unit disk with center $(1,0)$. Introducing polar coordinates we obtain $$J=\int_{-\pi/4}^{\pi/4}\int_{1/\cos\phi}^{2\cos\phi}{r\cos\phi-1\over r^2} r\>dr\ d\phi\ .$$ Here the inner integral evaluates to $$(2\cos^2\phi-1)-(\log 2+2\log\cos\phi)\ .$$ We therefore get $$J=1-{\pi\over2}\log 2-4\int_0^{\pi/4}\log\cos\phi\ d\phi=1+{\pi\over2}\log 2-2 \>{\tt Catalan}\doteq0.256862\ ,$$ where ${\tt Catalan}$ is Catalan's constant ($\doteq0.915966$)

Answer 2

The integrand function $\frac{y}{x^2+(y+1)^2}$ suggest to put $$\left\{ \begin{align} x&=r\cos\theta\\ y+1&=r\sin\theta \end{align}\right. $$ so that $x^2+(y+1)^2=r^2$ and the Jacobian is $r$.

From $y\ge 0$ we have $y=r\sin\theta-1\ge 0$ that is $r\ge\frac{1}{\sin\theta}$ and from $x^2+y^2\le 1$ we have $$x^2+y^2=r^2\cos^2\theta+(r\sin\theta-1)^2=r^2-2r\sin\theta+1\le 1$$ and then $r(r-2\sin\theta)\le0$ so that $r\le 2\sin\theta$. So we have $$\boxed{ r_{\min}=\frac{1}{\sin\theta}\le r\le 2\sin\theta=r_{\max}} $$ For $y=0$ (i.e. $r\sin\theta =1$) we have $-1\le x\le 1$, that is $-1\le r\cos\theta\le 1$ and then $-1\le\tan\theta\le 1$; thus $$\boxed{ \theta_{\min}=\frac{\pi}{4}\le \theta\le \frac{3\pi}{4}=\theta_{\max}} $$

or $\frac{-\pi}{4}\le \theta\le \frac{+\pi}{4}$ if you prefer.

The figure help to show all we have done.

So the integrand in polar coordinates becomes $f(r,\theta)=\frac{r\sin\theta-1}{r^2}$ and the integral becomes $$ \mathcal{I}=\int_{\theta_{\min}}^{\theta_{\max}}\int_{r_{\min}}^{r_{\max}} f(r,\theta)r\,\mathrm d r\,\mathrm d\theta= \int_{\frac{\pi}{4}}^{\frac{3\pi}{4}}\int_{\frac{1}{\sin\theta}}^{2\sin\theta}\left(\sin\theta-\frac{1}{r}\right) \mathrm d r\,\mathrm d\theta $$ The integral in $r$ is easy to evaluate $$\begin{align} \int_{\frac{1}{\sin\theta}}^{2\sin\theta}\left(\sin\theta-\frac{1}{r}\right) \mathrm d r &= \left[\sin\theta\, r-\log r\right]_{\frac{1}{\sin\theta}}^{2\sin\theta}\\ &=\sin\theta\left[2\sin\theta-\tfrac{1}{\sin\theta}\right]-\left[\log(2\sin\theta)-\log\left(\tfrac{1}{\sin\theta}\right)\right]\\ &=-\cos(2\theta)-\log\left(2\sin^2\theta\right) \end{align} $$ Then the integral in $\theta$ is $$\begin{align} \int_{\frac{\pi}{4}}^{\frac{3\pi}{4}} \left[-\cos(2\theta)-\log\left(2\sin^2\theta\right)\right]\mathrm d \theta &= \left[-\frac{1}{2}\sin(2\theta)\, \right]_{\frac{\pi}{4}}^{\frac{3\pi}{4}}-\int_{\frac{\pi}{4}}^{\frac{3\pi}{4}} \log\left(2\sin^2\theta\right)\mathrm d \theta=1+J \end{align} $$ where $$ J=-\int_{\frac{\pi}{4}}^{\frac{3\pi}{4}} \log\left(2\right)\mathrm d \theta-\int_{\frac{\pi}{4}}^{\frac{3\pi}{4}} \log\left(\sin^2\theta\right)\mathrm d \theta= -\frac{\pi}{2}\log 2-2C+\pi\log 2=\frac{\pi}{2}\log 2-2C $$ observig that $$\begin{align} -\int_{\frac{\pi}{4}}^{\frac{3\pi}{4}} \log\left(\sin^2\theta\right)\mathrm d \theta &= -\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \log\left(\cos^2\theta\right)\mathrm d \theta=-2\int_{0}^{\frac{\pi}{4}} \log\left(\cos^2\theta\right)\mathrm d \theta\\ &=-4\int_{0}^{\frac{\pi}{4}} \log\left(\cos\theta\right)\mathrm d \theta=-4\left(\frac{C}{2}-\frac{\pi}{4}\log 2\right)\\ &=-2C+\pi\log 2 \end{align} $$ where $C$ is the Catalan's constant (see for exaple here).

Finally we have $$\large\color{blue}{ \mathcal I=1+\frac{\pi}{2}\log 2-2C} $$