4

I have a valid proof for the Chain Rule, however I do not understand why the 'arguement' given here is incorrect.

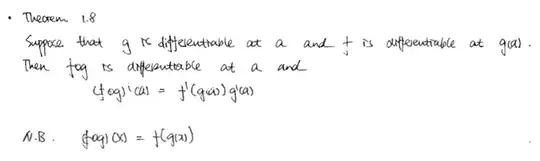
enter image description here

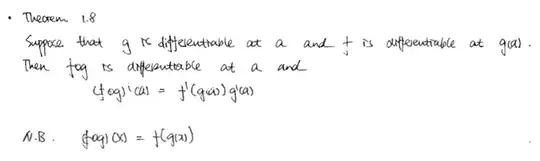
enter image description here

usainlightning
  • 1,217
  • 4
    It already says why: Consider constant $g$ as an extreme case. Do you see the deathly sin secretly commited in the proof? – k.stm Jan 20 '15 at 20:35

3 Answers3

9

One simple way to fix the problem of "division by zero" when $g(x)-g(a)=0$ is to define the continuous function $$ \frac{\Delta f}{\Delta g}(x)= \begin{cases} f'(g(a))&\quad\text{if }g(x)-g(a)=0\\ \\ \dfrac{f(g(x))-f(g(a))}{g(x)-g(a)}&\quad\text{otherwise} \end{cases} $$ and confirm (think it through properly) that we have $$ \frac{f(g(x))-f(g(a))}{x-a}=\frac{g(x)-g(a)}{x-a}\cdot\frac{\Delta f}{\Delta g}(x) $$ both for values of $x$ where $g(x)-g(a)=0$ and other values of $x$. In the first case, both sides becomes zero, and in the second case we are basically considering the dangerous step $$ \frac{f(g(x))-f(g(a))}{x-a}=\frac{g(x)-g(a)}{x-a}\cdot\frac{f(g(x))-f(g(a))}{g(x)-g(a)} $$ which is now legitimate since $g(x)-g(a)\neq 0$. When taking limits, you will need the continuity of $\dfrac{\Delta f}{\Delta g}(x)$.

String
  • 18,395
  • 2
    This avoids treating $g(x)=g(a)$ as a completely separate special case, and avoids introducing another elaborate mechanism, but it does require some careful thought (e.g. about the continuity of $\frac{\Delta f}{\Delta g}(x)$). – David K Mar 08 '15 at 13:41
  • I love this idea, but I have a slight hang up and I'm very hopeful that this will still be addressed on a post from several years ago. How do we know that $\lim\limits_{x \to a} \dfrac{f(g(x)) - f(g(a))}{g(x) - g(a)} = f'(g(a))$? Is this not separate from the definition of $f'(g(a))$, which is is that $\lim\limits_{x \to g(a)} \dfrac{f(x) - f(g(a))}{x - g(a)} = f'(g(a))$? This would be required for the term $g(x) - g(a)$ to cancel, yet I don't see why we have this. Can anyone point it out to me? – Thomas Winckelman Aug 02 '19 at 21:30
  • 1
    Wait, wow! I had an epiphany and figured it out! To the original poster of this answer: you are an angel, I've been stuck on this proof for weeks! I don't know why I haven't seen this idea before, it's both elegant and efficient. Here is a typed proof https://drive.google.com/open?id=15rm6Hwoe91eIQnfLrQD8h1enu5-E6hO7 which somewhat formalizes the argument. I f***ing love you for sharing this. Thank you! – Thomas Winckelman Aug 02 '19 at 22:51
  • 1
    @ThomasWinckelman: I am happy to read about that! An epiphany is such a pleasant moment. I tried to follow the link, but was blocked. Perhaps you could allow access for anyone with the link? – String Aug 03 '19 at 00:18
  • @String That's actually very good to know, this is the second time I've had trouble sharing links to my Google files. Does it still not work? Maybe this https://drive.google.com/file/d/15rm6Hwoe91eIQnfLrQD8h1enu5-E6hO7/view?usp=sharing will work, instead. – Thomas Winckelman Aug 03 '19 at 02:02
2

The problem is simply that if $g$ were constant in a neighborhood of $a$, then $g(x)-g(a)=0$ when $x$ is close to $a$, and thus you are dividing by $0$.

Daniel Robert-Nicoud
  • 29,795
0

I see that this is an old post, but I'm hoping I might get a response here anyway. As I'm working through this proof, I actually don't see why we need to define Δ/Δ to be a continuous function. It seems to me both that (i) Δ/Δ is always going to be equal to the difference quotient regardless of what value we assign to it in the case that g(x) = g(a) and (ii) the limit of Δ/Δ will always approach ′(()) as x approaches a, so I don't see the harm in choosing any arbitrary value for Δ/Δ when g(x) = g(a). Intuitively, I feel that there's something wrong with statement (ii), but I can't place a finger on precisely what's wrong with it.

Edit: Sorry, I meant to post this as a response to another comment, not as an answer. I am new to the website.

Dan1694
  • 43
  • Welcome to Math.SE! Please use MathJax. For some basic information about writing math at this site see e.g. basic help on mathjax notation, mathjax tutorial and quick reference, main meta site math tutorial and equation editing how-to. – GNUSupporter 8964民主女神 地下教會 Feb 26 '19 at 16:55
  • Hi, see this PDF https://drive.google.com/open?id=15rm6Hwoe91eIQnfLrQD8h1enu5-E6hO7 which you might or might not still find interesting. – Thomas Winckelman Aug 02 '19 at 22:53
  • It seems to me like the answer to your question is that, what we really need is that $\lim\limits_{x \to a} \dfrac{\Delta f}{\Delta g} = g'(f(a))$. The argument to show that this is true is somewhat similar to the argument that $\dfrac{\Delta f}{\Delta g}$ is continuous at $a$. In fact, there's a theorem which states that a function $f$ is continuous at a limit point $a$ of its domain if and only if $f(x) = f(a)$. – Thomas Winckelman Aug 02 '19 at 22:59
  • 1
    To be more precise (if I am not mistaken), we need that $\lim\limits_{x \to a} \dfrac{\Delta f}{\Delta g} = g'(f(a))$ in order to prove our desired convergence result, and this happens to be equivalent to saying that $\dfrac{\Delta f}{\Delta g}$ is continuous at $a$. Lastly, getting down to brass tacks, it turns out that we require that $\dfrac{\Delta f}{\Delta g}(x) = G$ when $f(x) = f(a)$ in order to prove that $\lim\limits_{x \to a} \dfrac{\Delta f}{\Delta g} = g'(f(a))$ (which is what we really care about). The details are presented in that PDF I shared a link to. – Thomas Winckelman Aug 02 '19 at 23:02
  • @ThomasWinckelman: Interesting to see your formal rendition of this! Cheers. – String Feb 20 '21 at 15:05
  • @Dan: I know that I am really late to this thread (as were you originally). Regarding (i), I believe that is false. When $g(x)=g(a)$ the difference quotient in question is NOT defined. Now we essentially have three scenarios: 1. It IS in fact defined for $x$ in some neighbourhood of $a$, 2. $g(x)=g(a)$ for $x$ in some neighbourhood of $a$, 3. The set for which $g(x)=g(a)$ accumulates at $a$ with $x=a$ as it's limit point. Case number 3 is the hardest and highlights the problem: The split into a product of fractions may not be defined near the limit. – String Feb 20 '21 at 15:18