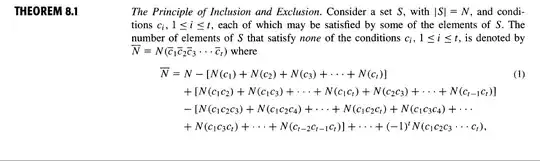4

Inclusion Exclusion Used

enter image description here

Theorem 8.1

enter image description here

The Question:

In how many ways can one distribute $10$ distinct prizes to $4$ students with exactly $2$ students getting nothing. b) How many ways have at least 2 students receiving prizes?

My Work:

Let $S =$ {All ways to distribute the prizes}

$|S|= 10^4$

$A =$ student 1 gets a prize

$B =$ student 2 gets a prize

$C =$ student 3 gets a prize

$D =$ student 4 gets a prize

By the Inclusion-Exclusion** formula given, our answer is:

$S_2 - \binom{3}{1}S_3 + \binom{4}{2}S_4$

$S_2 = 100*6 =$ all distinct unions between 2 sets summed together

$S_3 = 1000*4$ all distinct unions between 3 of our sets summed together

$600-4*1000*4+C(4,2)*10000 = 44'600$

My Question

I don't think how I'm doing this question is right because I got the wrong answer from the back of my book. I'm wondering where I went wrong.

Dunka
  • 2,787
  • 12
  • 41
  • 69
  • 1
    I don't know whether you have to use the formula. If you do not, let the students be A, B, C, D. The sad students who get nothing can be chosen in $\binom{4}{2}$ ways. For each way, the higher remaining student in the alphabet can be prized in $2^{10}-2$ ways, all but the empty set and the full set. – André Nicolas Jan 24 '15 at 04:15
  • Please state the "hypotheses of theorem 8.1" – Thomas Andrews Jan 24 '15 at 04:27
  • @ThomasAndrews I made the edit. Andre, thank you. I would like to understand how to use the formula the book has though – Dunka Jan 24 '15 at 04:33
  • Where you have $10^4$ up there, should it be $4^{10}$? – turkeyhundt Jan 24 '15 at 04:54
  • @turkeyhundt my reasoning was I could put 10 distinct objects into 4 distinct boxes, which I think I can do 101010*10 ways because there are 10 possibilities for each box(student) – Dunka Jan 24 '15 at 04:56
  • I think it's the other way around. Each of the 10 prizes can be won by any of the 4 students. $10^4$ would be a situation where each student could only get one prize and a prize can be awarded multiple times. – turkeyhundt Jan 24 '15 at 04:58
  • I think you are right, thank you. – Dunka Jan 24 '15 at 05:01

2 Answers2

3

A little late, but for the sake of completeness, here is the correct way to use the formula.

You're looking for $E_2$ (exactly 2 students getting nothing). Applying the formula directly, and as you already stated, you get:

$$E_2 = S_2 - \binom{3}{1}S_3 + \binom{4}{2}S_4$$

Now you need to compute $S_2$, $S_3$ and $S_4$.

Let $c_1$ be the case where student 1 gets nothing, $c_2$ the case where student 2 gets nothing, same pattern for $c_3$ and $c_4$. To apply the formula, we are interested in the cases where 2 students get nothing (for instance, $N(c_1c_2)$), the cases where 3 students get nothing (for instance, $N(c_1c_2c_3)$), and finally the cases where 4 students get nothing (that is: $N(c_1c_2c_3c_4)$

If student 1 and student 2 get nothing, that means that all prizes are given to the 2 other students: $N(c_1c_2) = 2^{10}$. Same thing for all other combinations of 2 students, and there are $\binom{4}{2}$ of them. This leads to:

$$S_2 = \binom{4}{2}2^{10}$$

If student 1, student 2 and student 3 get nothing, that means that all prizes are given to the last student: $N(c_1c_2c_3) = 1^{10}$. Same thing for all other combinations of 3 students, and there are $\binom{4}{3}$ of them:

$$S_3 = \binom{4}{3}1^{10}$$

$S_4$ counts the ways nobody gets any prize. This is not possible, as all prizes must be distributed:

$$S_4 = 0$$

Plugging that into the initial formula gives you the right answer:

$$E_2 = \binom{4}{2}2^{10} - \binom{3}{1}\binom{4}{3}1^{10} + \binom{4}{2}0 = 6132$$

By the way, turkeyhundt is right, there are of course $4^{10}$ ways to give the 10 prizes to the 4 students, not $10^4$. Even if that value is not needed here, the same reasoning is used to compute $S_2$ and $S_3$.

Georges
  • 31
2

Is the answer 6132?

${4\choose 2}=6$ ways to pick the two students who get a prize. Then the 10 prizes can each go to one of those two students, with the exceptions of the two cases where one student gets all of the prizes.

So $6\times1022=6132$?

turkeyhundt
  • 7,733