Crossed Ladders Problem

Question

I tried to use the angles ($\cos$ and $\tan$) and the Intercept theorem but I don't know where is the trench in the figure. Is it just the base?

• Could someone write down the steps by drawing each figure that's gonna be needed in your proof?

I think it usually leads to polynomial equations of degree 4:

$$x^4-6x^3-36x^2+216x-324=0$$

but I'm not sure and I need the steps for writing it in LaTex.

I think it is about $$6,326 m $$ by using Newton's method.

Answer 1

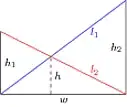
There is no need to use trigonometry here: the Intercept theorem leads to the first equation of $\left(1\right)$ and the Pythagorean theorem leads to the second and third equations of $\left(1\right)$.
The crossed ladders problem is a special case of the system of equations $\left(1\right)$.

\begin{equation} \begin{split} h_1h_2&=h\left(h_1+h_2\right)\\ h_1^2&=l_2^2-w^2\\ h_2^2&=l_1^2-w^2\\ \end{split} \tag 1 \end{equation}

$h$, $l_1$, and $l_2$ are known real numbers.
$h_1$, $h_2$, and $w$ are unknown complex numbers.
The general analytical solution can be found as shown below and applied to any such problem.

Solving the general case

Let $\left(j,k\right)\in\lbrace\left(1,2\right),\left(2,1\right)\rbrace$.
Let the real numbers:

\begin{equation} \begin{split} c_{jA}&=l_j^2-l_k^2\\ c_{jB}&=3\left(2c_{jA}-3h^2\right)\\ c_{jC}&=c_{jA}\left(c_{jA}^2+54h^4\right)\\ c_{jD}&=6h^4c_{jA}\left(c_{jA}^2+2h^2c_{jA}+h^4\right)\\ c_{jE}&=c_{jA}\left(c_{jA}^5-3h^2c_{jA}^4+39h^4c_{jA}^3-91h^6c_{jA}^2+324h^8c_{jA}-54h^{10}\right)\\ c_F&=9\left(l_j^2+l_k^2-2h^2\right)\\ c_G&=3\left(c_{jA}^2+12h^4\right)\\ c_H&=3\left(c_{jA}^2+27h^4\right)\\ c_I&=c_{jA}^2\left(c_{jA}^4+36h^4c_{jA}^2+216h^8\right)\\ c_J&=96h^6\left( \begin{split} &4h^8c_{jA}^4+2h^4\left(l_j^4-l_k^4\right)\left(l_j^4+6l_j^2l_k^2+l_k^4\right)\left(4h^2c_{jA}-3l_j^4+3l_k^4\right)\\ &+h^2\left(l_j^4-l_k^4\right)^2\left(l_j^2+l_k^2\right)\left(l_j^4+10l_j^2l_k^2+l_k^4\right)-l_j^2l_k^2\left(l_j^4-l_k^4\right)^2\left(l_j^2+l_k^2\right)^2\\ \end{split} \right)\\ c_K&=\left( \begin{split} &\left(l_j^4-l_k^4\right)^5\left(l_j^4-l_k^4-12h^2c_{jA}\right) +48h^4\left(l_j^4-l_k^4\right)^4\left(2l_j^4-l_j^2l_k^2+2l_k^4\right)\\ &-16h^6c_{jA}\left(l_j^4-l_k^4\right)^3\left(37l_j^4+34l_j^2l_k^2+37l_k^4\right)\\ &+48h^8\left(l_j^4-l_k^4\right)^2\left(53l_j^8-2l_j^6l_k^2-30l_j^4l_k^4-2l_j^2l_k^6+53l_k^8\right)\\ &-96h^{10}c_{jA}\left(l_j^4-l_k^4\right)\left(83l_j^8+100l_j^6l_k^2+66l_j^4l_k^4+100l_j^2l_k^6+83l_k^8\right)\\ &+256h^{12}c_{jA}^2\left(70l_j^8+161l_j^6l_k^2+186l_j^4l_k^4+161l_j^2l_k^6+70l_k^8\right)\\ &-6912h^{14}c_{jA}\left(l_j^4-l_k^4\right)\left(3l_j^4+2l_j^2l_k^2+3l_k^4\right)+3456h^{16}c_{jA}^4\\ \end{split} \right)\\ R_{j1}&=3\sqrt[3]{c_{jC}+6h^2c_{jA}\sqrt{c_H}}+3\sqrt[3]{c_{jC}-6h^2c_{jA}\sqrt{c_H}}\\ R_{j2}&=\ \text{sgn}\left(hc_{jA}+h^3\right)\sqrt{R_{j1}-c_{jB}}\\ R_{j3}&=6\sqrt{3\sqrt[3]{c_{jE}+c_{jD}\sqrt{c_H}}+3\sqrt[3]{c_{jE}-c_{jD}\sqrt{c_H}}+3c_{jA}^2-12h^2c_{jA}+9h^4}\\ R_{j4}&=\sqrt{R_{j3}-R_{j1}-2c_{jB}}\\ R_{j5}&=\left(-1\right)^j\sqrt{R_{j3}+R_{j1}+2c_{jB}}\\ R_6&=3\sqrt[3]{c_I+24h^6c_{jA}^2\sqrt{c_H}}+3\sqrt[3]{c_I-24h^6c_{jA}^2\sqrt{c_H}}\\ R_7&=3\sqrt{R_6+c_G}\\ R_8&=6\ \text{sgn}\left(3h+R_{j2}\right)\sqrt{2c_G-R_6+12\left|h\right|^3\sqrt{ \begin{split} &36h^2-6\sqrt[3]{27h^2c_{jA}^2+3c_{jA}^2\sqrt{c_H}}\\ &-6\sqrt[3]{27h^2c_{jA}^2-3c_{jA}^2\sqrt{c_H}}\\ \end{split} }}\\ R_9&=3\sqrt{ \begin{split} &6\ \text{sgn}\left(R_8^2+8c_FR_7+36R_6-72c_G\right)\sqrt{ \begin{split} &3\sqrt[3]{c_K+c_J\sqrt{c_H}}+3\sqrt[3]{c_K-c_J\sqrt{c_H}}\\ &+3\left(l_j^4-l_k^4\right)^2-12h^2c_{jA}\left(l_j^4-l_k^4\right)\\ &+48h^4\left(l_j^4+l_j^2l_k^2+l_k^4\right)\\ \end{split} }\\ &+2R_6+6\left(l_j^4+4l_j^2l_k^2+l_k^4\right)-36h^2\left(l_j^2+l_k^2\right)\\ \end{split} }\\ c_L&=1-\left(-1\right)^j\ \text{sgn}\left(3h-R_{j2}\right)-\left|\ \text{sgn}\left(3h-R_{j2}\right)\right|\\ c_M&=1+\left(-1\right)^j\ \text{sgn}\left(3h-R_{j2}\right)-\left|\ \text{sgn}\left(3h-R_{j2}\right)\right|\\ c_N&=\frac{1+\ \text{sgn}\left(2c_F-2R_7+R_8\right)}{2}\\ c_O&=\frac{1-\ \text{sgn}\left(2c_F-2R_7+R_8\right)}{2}\\ c_P&=\frac{1+\ \text{sgn}\left(2c_F-2R_7-R_8\right)}{2}\\ c_Q&=\frac{1-\ \text{sgn}\left(2c_F-2R_7-R_8\right)}{2}\\ \end{split} \notag \end{equation}

According to the first equation of $\left(1\right)$:

\begin{equation} h_k\left(h_j-h\right)=hh_j \notag \end{equation}

Squaring this last equation:

\begin{equation} h_k^2\left(h_j^2-2hh_j+h^2\right)=h^2h_j^2 \tag 2 \end{equation}

Combining the last two equations of $\left(1\right)$:

\begin{equation} h_k^2=h_j^2+c_{jA} \notag \end{equation}

Combining this last equation with $\left(2\right)$:

\begin{equation} h_j^4-2hh_j^3+c_{jA}h_j^2-2hc_{jA}h_j+h^2c_{jA}=0 \tag 3 \end{equation}

Let $h_{j1}$, $h_{j2}$, $h_{j3}$, and $h_{j4}$ be the solutions to $\left(3\right)$:

\begin{equation} \left(h_j-h_{j1}\right)\left(h_j-h_{j2}\right)\left(h_j-h_{j3}\right)\left(h_j-h_{j4}\right)=0 \tag 4 \end{equation}

Let the complex numbers $x_{j1}$, $x_{j2}$, and $x_{j3}$ be such that:

\begin{equation} \begin{split} h_{j1}&=\frac{3h+\left(-1\right)^j\left(\sqrt{x_{j1}}-\sqrt{x_{j2}}\right)-\ \text{sgn}\left(hc_{jA}+h^3\right)\sqrt{x_{j3}}}{6}\\ h_{j2}&=\frac{3h-\left(-1\right)^j\left(\sqrt{x_{j1}}-\sqrt{x_{j2}}\right)-\ \text{sgn}\left(hc_{jA}+h^3\right)\sqrt{x_{j3}}}{6}\\ h_{j3}&=\frac{3h-\sqrt{x_{j1}}-\sqrt{x_{j2}}+\ \text{sgn}\left(hc_{jA}+h^3\right)\sqrt{x_{j3}}}{6}\\ \end{split} \notag \end{equation}

Expanding $\left(4\right)$ and equating its coefficients with the ones of $\left(3\right)$:

\begin{equation} \begin{split} h_{j4}&=\frac{3h+\sqrt{x_{j1}}+\sqrt{x_{j2}}+\ \text{sgn}\left(hc_{jA}+h^3\right)\sqrt{x_{j3}}}{6}\\ c_{jA}&=\frac{27h^2-\left(x_{j1}+x_{j2}+x_{j3}\right)}{18}\\ 2hc_{jA}&=\frac{27h^3-3h\left(x_{j1}+x_{j2}+x_{j3}\right)+2\ \text{sgn}\left(hc_{jA}+h^3\right)\sqrt{x_{j1}}\sqrt{x_{j2}}\sqrt{x_{j3}}}{54}\\ h^2c_{jA}&=\frac{1}{1296}\left( \begin{split} &\left(9h^2-\left(x_{j1}+x_{j2}+x_{j3}\right)\right)^2+24h\ \text{sgn}\left(hc_{jA}+h^3\right)\sqrt{x_{j1}}\sqrt{x_{j2}}\sqrt{x_{j3}}\\ &-4\left(x_{j1}x_{j2}+x_{j1}x_{j3}+x_{j2}x_{j3}\right)\\ \end{split} \right)\\ \end{split} \notag \end{equation}

Combining these last three equations:

\begin{equation} \begin{split} x_{j1}+x_{j2}+x_{j3}&=-3c_{jB}\\ \ \text{sgn}\left(hc_{jA}+h^3\right)\sqrt{x_{j1}}\sqrt{x_{j2}}\sqrt{x_{j3}}&=27h\left(c_{jA}+h^2\right)\\ x_{j1}x_{j2}+x_{j1}x_{j3}+x_{j2}x_{j3}&=3\left(c_{jB}^2-9c_{jA}^2\right)\\ \end{split} \tag 5 \end{equation}

$x_{j1}$, $x_{j2}$, and $x_{j3}$ are the solutions to the equation of unknown $x_j$:

\begin{equation} \left(x_j-x_{j1}\right)\left(x_j-x_{j2}\right)\left(x_j-x_{j3}\right)=0 \notag \end{equation}

Expanding this last equation:

\begin{equation} x_j^3+3c_{jB}x_j^2+3\left(c_{jB}^2-9c_{jA}^2\right)x_j-729h^2\left(c_{jA}+h^2\right)^2=0 \notag \end{equation}

Let $\text{i}$ be the imaginary unit.
Let the complex numbers $y_{j1}$ and $y_{j2}$ be such that:

\begin{equation} \begin{split} x_{j1}&=\frac{3\left(\text{i}\sqrt{3}-1\right)\sqrt[3]{y_{j1}}-3\left(\text{i}\sqrt{3}+1\right)\sqrt[3]{y_{j2}}-2c_{jB}}{2}\\ x_{j2}&=\frac{3\left(\text{i}\sqrt{3}-1\right)\sqrt[3]{y_{j2}}-3\left(\text{i}\sqrt{3}+1\right)\sqrt[3]{y_{j1}}-2c_{jB}}{2}\\ \end{split} \notag \end{equation}

Combining these last two equations with $\left(5\right)$:

\begin{equation} \begin{split} x_{j3}&=3\sqrt[3]{y_{j1}}+3\sqrt[3]{y_{j2}}-c_{jB}\\ 729h^2\left(c_{jA}+h^2\right)^2&=27\left(y_{j1}+y_{j2}\right)-c_{jB}^3+27c_{jB}\sqrt[3]{y_{j1}}\sqrt[3]{y_{j2}}\\ 3\left(c_{jB}^2-9c_{jA}^2\right)&=3c_{jB}^2-27\sqrt[3]{y_{j1}}\sqrt[3]{y_{j2}}\\ \end{split} \notag \end{equation}

Combining these last two equations:

\begin{equation} \begin{split} y_{j1}+y_{j2}&=2c_{jC}\\ \sqrt[3]{y_{j1}}\sqrt[3]{y_{j2}}&=c_{jA}^2\\ \end{split} \tag 6 \end{equation}

$y_{j1}$ and $y_{j2}$ are the solutions to the equation of unknown $y_j$:

\begin{equation} \left(y_j-y_{j1}\right)\left(y_j-y_{j2}\right)=0 \notag \end{equation}

Expanding this last equation:

\begin{equation} y_j^2-2c_{jC}y_j+c_{jA}^6=0 \notag \end{equation}

Let the complex number $z_{j1}$ be such that:

\begin{equation} y_{j1}=c_{jC}+\sqrt{z_{j1}} \notag \end{equation}

Combining this last equation with $\left(6\right)$:

\begin{equation} \begin{split} y_{j2}&=c_{jC}-\sqrt{z_{j1}}\\ c_{jA}^6&=c_{jC}^2-z_{j1}\\ \end{split} \notag \end{equation}

Solving this last equation:

\begin{equation} z_{j1}=36h^4c_{jA}^2c_H \notag \end{equation}

Thus:

\begin{equation} \begin{split} y_{j1}&=c_{jC}+6h^2\left|c_{jA}\right|\sqrt{c_H}\\ y_{j2}&=c_{jC}-6h^2\left|c_{jA}\right|\sqrt{c_H}\\ \end{split} \notag \end{equation}

Thus:

\begin{equation} \begin{split} x_{j1}&=\frac{3\left(\text{i}\sqrt{3}-1\right)\sqrt[3]{c_{jC}+6h^2\left|c_{jA}\right|\sqrt{c_H}}-3\left(\text{i}\sqrt{3}+1\right)\sqrt[3]{c_{jC}-6h^2\left|c_{jA}\right|\sqrt{c_H}}-2c_{jB}}{2}\\ x_{j2}&=\frac{3\left(\text{i}\sqrt{3}-1\right)\sqrt[3]{c_{jC}-6h^2\left|c_{jA}\right|\sqrt{c_H}}-3\left(\text{i}\sqrt{3}+1\right)\sqrt[3]{c_{jC}+6h^2\left|c_{jA}\right|\sqrt{c_H}}-2c_{jB}}{2}\\ x_{j3}&=3\sqrt[3]{c_{jC}+6h^2\left|c_{jA}\right|\sqrt{c_H}}+3\sqrt[3]{c_{jC}-6h^2\left|c_{jA}\right|\sqrt{c_H}}-c_{jB}\\ \end{split} \notag \end{equation}

Thus:

\begin{equation} \begin{split} h_{j1}&=\frac{3h-R_{j2}}{6}+\text{i}\frac{R_{j5}}{6}\\ h_{j2}&=\frac{3h-R_{j2}}{6}+\text{i}\frac{-R_{j5}}{6}\\ h_{j3}&=\frac{3h+R_{j2}-R_{j4}}{6}\\ h_{j4}&=\frac{3h+R_{j2}+R_{j4}}{6}\\ \end{split} \tag 7 \end{equation}

According to the last two equations of $\left(1\right)$:

\begin{equation} w^2=l_k^2-h_j^2 \notag \end{equation}

Let $m\in\lbrace1,2,3,4\rbrace$.
Let the complex numbers $w_{m+}$ and $w_{m-}$ be such that:

\begin{equation} \begin{split} w_{m+}&=\sqrt{l_k^2-h_{jm}^2}\\ w_{m-}&=-\sqrt{l_k^2-h_{jm}^2}\\ \end{split} \notag \end{equation}

Combining these last two equations with $\left(7\right)$:

\begin{equation} \begin{split} w_{1+}&=\frac{\sqrt{R_9+R_7+c_F}}{6}+\text{i}\frac{c_L\sqrt{R_9-R_7-c_F}}{6}\\ w_{1-}&=\frac{-\sqrt{R_9+R_7+c_F}}{6}+\text{i}\frac{-c_L\sqrt{R_9-R_7-c_F}}{6}\\ w_{2+}&=\frac{\sqrt{R_9+R_7+c_F}}{6}+\text{i}\frac{c_M\sqrt{R_9-R_7-c_F}}{6}\\ w_{2-}&=\frac{-\sqrt{R_9+R_7+c_F}}{6}+\text{i}\frac{-c_M\sqrt{R_9-R_7-c_F}}{6}\\ w_{3+}&=\frac{c_N\sqrt{\left|2c_F-2R_7+R_8\right|}}{6}+\text{i}\frac{c_O\sqrt{\left|2c_F-2R_7+R_8\right|}}{6}\\ w_{3-}&=\frac{-c_N\sqrt{\left|2c_F-2R_7+R_8\right|}}{6}+\text{i}\frac{-c_O\sqrt{\left|2c_F-2R_7+R_8\right|}}{6}\\ w_{4+}&=\frac{c_P\sqrt{\left|2c_F-2R_7-R_8\right|}}{6}+\text{i}\frac{c_Q\sqrt{\left|2c_F-2R_7-R_8\right|}}{6}\\ w_{4-}&=\frac{-c_P\sqrt{\left|2c_F-2R_7-R_8\right|}}{6}+\text{i}\frac{-c_Q\sqrt{\left|2c_F-2R_7-R_8\right|}}{6}\\ \end{split} \notag \end{equation}

Let $n\in\lbrace-,+\rbrace$.
The solutions to $\left(1\right)$ are the eight triplets $\left(h_{jm},h_{km},w_{mn}\right)$.

Applying the solution to the given problem

Let $h=3\ m$, $l_j=8\ m$, and $l_k=10\ m$.
The values in the only triplet containing only real positive values are:

\begin{equation} \begin{split} R_{k1}^{'}&=6\sqrt[3]{35+3\sqrt{129}}+6\sqrt[3]{35-3\sqrt{129}}\\ R_6^{'}&=3\sqrt[3]{262+6\sqrt{129}}+3\sqrt[3]{262-6\sqrt{129}}\\ h_{j4}&=\frac{3-\sqrt{33-R_{k1}^{'}}+\sqrt{66+R_{k1}^{'}+6\sqrt{105+6\sqrt[3]{3547+27\sqrt{129}}+6\sqrt[3]{3547-27\sqrt{129}}}}}{2}\\ &\approx7,7446378738165\ m\\ h_{k4}&=\frac{\sqrt{6\sqrt{6\sqrt[3]{1269+75\sqrt{129}}+6\sqrt[3]{1269-75\sqrt{129}}+9}-R_{k1}^{'}-30}+\sqrt{R_{k1}^{'}-15}+3}{2}\\ &\approx4,8968781684408\ m\\ w_{4+}&=\sqrt{73-3\sqrt{21+R_6^{'}}-3\sqrt{42-R_6^{'}+6\sqrt{9-3\sqrt[3]{54+6\sqrt{129}}-3\sqrt[3]{54-6\sqrt{129}}}}}\\ &\approx6,3261824352012\ m\\ \end{split} \notag \end{equation}