I'm trying to solve
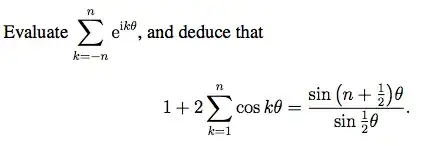
So far I've done the first part, evaluating the summation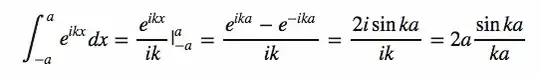 
;
where a is just n. I'm not sure where to go from here or what it even means deduce the second summation. I understand that the summation of simply $$\sum\limits_{k=0}^n\cos(kx)$$ is derived from looking at the real part of $$\sum_{k=0}^n{\rm e}^{ikx} $$I'm guessing they want me to see how the second summation in the question is defined by 'playing around' with the original?
Setting $z=e^{i\theta}$, so that $2\cos k\theta={z^k+z^{-k}}$, we have $$1+2\cos\theta+2\cos2\theta+\dots2\cos k\theta=1+z+z^{-1}+z^2+z^{-2}+\dots z^k+z^{-k}.$$
This geometric series runs from $z^{-k}$ to $z^k$, hence its sum is $$z^{-k}\frac{z^{2k+1}-1}{z-1}=\frac{z^{k+1}-z^{-k}}{z-1}=\frac{z^{k+1/2}-z^{-k-1/2}}{z^{1/2}-z^{-1/2}}=\frac{\sin(k+\frac12)\theta}{\sin\frac12\theta}.$$ (The trick is to divide up and down by $z^{1/2}$ to let sines appear.)
The first sum you are giving can be written as $$ \sum_{k=-n}^ne^{ik\theta} = \sum_{k=-n}^0e^{ik\theta} + \sum_{k=1}^ne^{ik\theta} = 1+\sum_{k=1}^ne^{-ik\theta} + \sum_{k=1}^ne^{ik\theta} = 1+\sum_{k=1}^n\bigl(e^{ik\theta}+e^{-ik\theta}\bigr) $$ Recall that $\cos(x) = \frac{e^{ix}+e^{-ix}}{2}$ so we have $$ 1+\sum_{k=1}^n\bigl(e^{ik\theta}+e^{-ik\theta}\bigr) = 1 +2\sum_{k=1}^n\cos(k\theta)\tag{1} $$
Let's just focus on the $\sum_{k=1}^n\cos(k\varphi)$ term and consider the series with $+i\sin(k\varphi)$.
\begin{align*} \cos(\varphi) + i\sin(\varphi) + \cdots + \cos(n\varphi) + i\sin(n\varphi) & = e^{i\varphi} + e^{2i\varphi} + \cdots + e^{ni\varphi}\\ & = \sum_{k = 1}^ne^{ki\varphi}\\ & = e^{i\varphi}\frac{1 - e^{i\varphi(n + 1)}}{1 - e^{i\varphi}}\\ & = e^{i\varphi}\frac{e^{i\varphi(n + 1)} - 1}{e^{i\varphi} - 1} \end{align*} Note that $\sin(\frac{\theta}{2}) = \frac{e^{i\theta/2} - e^{-i\theta/2}}{2i}$ so $2ie^{i\theta/2}\sin(\frac{\theta}{2}) = e^{i\theta} - 1$. \begin{align*} \sum_{k = 1}^ne^{ki\varphi} & = e^{i\varphi}\frac{e^{i\varphi(n + 1)/2}\sin\bigl(\frac{\varphi(n + 1)}{2}\bigr)} {e^{i\varphi/2}\sin\bigl(\frac{\varphi}{2}\bigr)}\\ & = \frac{\sin\bigl(\frac{\varphi(n + 1)}{2}\bigr)} {\sin\bigl(\frac{\varphi}{2}\bigr)}e^{in\varphi/2+i\varphi} \end{align*} By taking the real and imaginary parts of, we get the series for $\sum_{k = 1}^n\cos(n\varphi)$ and $\sum_{k = 1}^n\sin(n\varphi)$, respectively. \begin{align*} \sum_{k = 1}^n\cos(k\varphi) & = \frac{\sin\bigl(\frac{\varphi(n + 1)}{2}\bigr)} {\sin\bigl(\frac{\varphi}{2}\bigr)}\cos\Bigl(\frac{(n+1)\varphi}{2}\Bigr)\\ \sum_{k = 1}^n\sin(n\varphi) & = \frac{\sin\bigl(\frac{\varphi(n + 1)}{2}\bigr)} {\sin\bigl(\frac{\varphi}{2}\bigr)}\sin\Bigl(\frac{(n+1)\varphi}{2}\Bigr) \end{align*} Plugging back into $(1)$, we get $$ 1 +2\sum_{k=1}^n\cos(k\theta) = 1 + 2\frac{\sin\bigl(\frac{\varphi(n + 1)}{2}\bigr)} {\sin\bigl(\frac{\varphi}{2}\bigr)}\cos\Bigl(\frac{(n+1)\varphi}{2}\Bigr)\tag{2} $$ By exploiting the identity $\sin(a+b)=\sin(a)\cos(b)+\sin(b)\cos(a)$ in equation $(2)$, we can obtain $$ 1+2\sum_{k=1}^{n}\cos(k\theta) = \frac{\sin[(n+1/2)\varphi]}{\sin(\varphi/2)} $$
For the left side of the equation notice that
$$ \sum_{k=-n}^n e^{ikx} \;\; =\;\; e^{-inx} + e^{-i(n-1)x} + \ldots + e^{-ix} + 1 + e^{ix} + \ldots + e^{inx}. $$
This sum can be rearranged into $1 + 2 \sum_{k=1}^n \cos(kx)$. Do you see how? For the other part we can factor a term out of this finite sum, namely
$$ \sum_{k=-n}^n e^{ikx} \;\; =\;\; e^{-inx} (1 + e^{ix} + e^{i2x} + \ldots + e^{i2nx}). $$
The sum in the parentheses can be evaluated into a more concise expression (if the sum equals $s$ then consider the quantity $s-e^{ix}s$). Multiply the value of $s$ by the term on the outside, $e^{-inx}$, and this can be rearranged to obtain $\frac{\sin\left (n + \frac{1}{2}\right ) \theta}{\sin \frac{1}{2} \theta}$.
