4

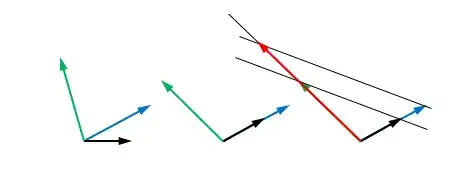
When dealing with complex numbers they can be presented as vectors, at least that is stated in my textbook. And the addition operation defined for complex numbers:

$$z_1 + z_2 = x_1 + x_2 + i(y_1 + y_2)$$

fully corresponds with the rules for vector addition.

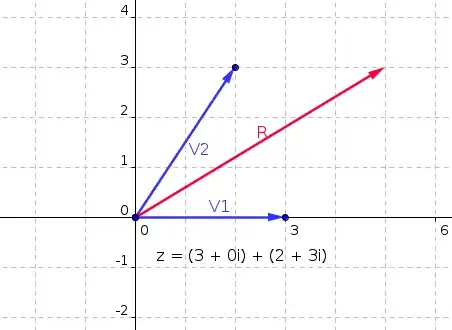
geometric representation of complex number addition

But why the multiplication operation does not have a geometric (vector) representation? I wonder, because my textbook states that $\sqrt{i} = e^{\frac{i\pi}{4}}, e^{\frac{i5\pi}{4}}$, that is:

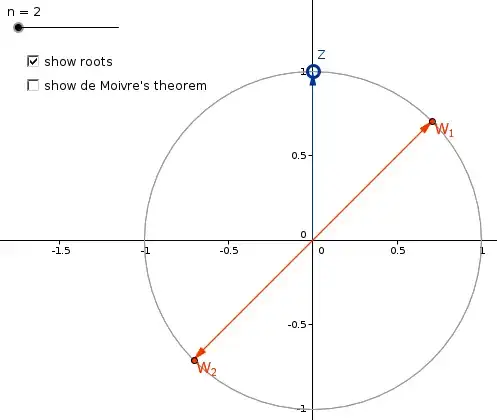
complex roots of imaginary one

But if I try to multiply $W_1 \times W_2$ I will get a zero vector. And even if $W_1$ and $W_2$ were not collinear I would have get a vector which lies in another plane.

So, could anyone give me an answer about whether I'm correct at all and if I am whether any explanation of this situation exists, or may be I just have to live with it?

Thank you.

d.k
  • 895
  • 2
  • 9
  • 19
  • 2
    If you can get hold of Needham's book Visual Complex Analysis, this is very well explained in section 1.I (see especially 1.I.5 on pp. 8–10). – Hans Lundmark Feb 04 '15 at 11:12

2 Answers2

9

In order to understand multiplication of complex numbers, it is better to represent complex numbers in "polar" form, namely $$ z=r(\cos(\theta)+i\sin(\theta)) $$ where $r$ is a positive real number representing the length of the vector defined by $z$ in the complex plane and $\theta$ the angle it forms with the real axis.

When you multiply $z$ with a similarly written $z^\prime$ and perform all the algebra you eventually get $$ zz^\prime=rr^\prime(\cos(\theta+\theta^\prime)+i\sin(\theta+\theta^\prime)) $$ The geometrical interpretation of multiplication is now very visible. E.g. if $|z^\prime|=1$ (i.e. $r^\prime=1$) multiplication by $z^\prime$ is just rotation by some angle.

AdLibitum
  • 3,003
2

Complex multiplication has no connection to the cross product of vectors.

You can understand complex multiplication as an addition in the logarithmic domain (the log of a complex number is the log of its module plus $i$ times the argument): you multiply the modules together and you add the arguments.

In geometric terms, one of the numbers applies a similarity transform to the other (scaling and rotation). Unfortunately, this interpretation is asymmetric. It is constructible with a ruler and a compass.

enter image description here

Take the green ($z_1$) and black ($1$) vectors and rotate them to align on the blue ($z_2$) one; this adds the arguments. Then by an homothety, you multiply the lengths and get the red ($z_1z_2$) vector.

  • okay, thank you, so I've understood that the statement that a complex number can be represented by a vector is incorrect. Please correct me, if I'm wrong – d.k Feb 04 '15 at 10:38
  • 2
    Complex numbers are commonly represented as 2D vectors, but the usual dot and cross products do not apply. (Actually, they are the real and imaginary parts of $z_1z_2^*$.) –  Feb 04 '15 at 11:05