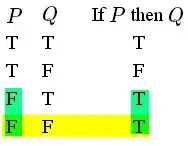
We can try with a formal argument.
Assume the definition :
$Z=\cap_{i \in I} \alpha_i=\{ x : ∀i \in I,x \in α_i \}$.
We know the basic property of the "set-builder" notation : $\{ x : \varphi \}$, i.e. $x \in \{ x : \varphi \} \Leftrightarrow \varphi(x)$.
Thus, we have :
$x \in Z \Leftrightarrow \forall i (i \in I \Rightarrow x \in α_i)$ --- (*)
(I'll prefer to be pedantic and avoid the use of "restricted quantifiers").
The formula (*) is a bi-conditional and "it works" like an axiom, stating the basic property of the defined symbol $Z$, "naming" the set built-up from the intersection of the "family" of sets : $\alpha_i, i \in I$.
The bi-conditional means also that, every time we have : $\forall i (i \in I \Rightarrow x \in α_i)$, we can derive : $x \in Z$ by modus ponens.
Now for the proof :
1) $I = \emptyset$ --- assumption : the "index-set" is empty
2) $\forall i (i \notin I)$ --- from 1) by definition of empty set
3) $i \notin I$ --- from 2) and the logical axiom : $\forall x \alpha \Rightarrow \alpha^x_t$ by modus ponens, where $\alpha^x_t$ is the result of the replacement of the occurrences of the variable $x$ in $\alpha$ with the term $t$
4) $(i \in I \Rightarrow x \in α_i)$ --- from 3) and the tautology : $\lnot p \Rightarrow (p \Rightarrow q)$ by modus ponens, where we have $i \in I$ in place of $p$ and $x \in \alpha_i$ in place of $q$
5) $\forall i (i \in I \Rightarrow x \in α_i)$ --- from 4) by generalization
6) $x \in Z$ --- from 5) and the axiom (*) by modus ponens
7) $\forall x(x \in Z)$ --- from 6) by generalization.
Thus, having assumed the axiom (*) corresponding to the definition, we have derived, "by logic alone", that :
if $I= \emptyset$ (i.e. the set $I$ is empty),then for all $x$, $x$ belongs to the set $Z=\cap_{i \in I} \alpha_i$.
Your "counterargument" is something like :
1) assume : $x \in Z \Rightarrow \forall i (i \in I \Rightarrow x \in α_i)$
and try to "contrapose" it, in order to derive $x \notin Z$.
But the negation of the consequent of 1) is :
$\lnot \forall i (i \in I \Rightarrow x \in α_i)$ i.e. $\exists i (i \in I \land x \notin α_i)$.
Now we assume :
2) $I=\emptyset$, i.e. $\forall i(i \notin I)$, i.e. $\forall i \lnot (i \in I)$.
But from the fact that : for no $i$ : $i \in I$, we cannot derive that there is some $i$ such that $i \in I$, and thus we cannot derive : there is some $i$ such that $(i \in I$ and ...) either.
You are saying :
"$I=\emptyset$, so there do not exist any sets $α_i$ for $x$ to be a member of";
we can formalize it as : $\forall x \lnot \exists i (x \in \alpha_i)$, i.e. : $\forall x \forall i (x \notin \alpha_i)$.
But again, $\forall i (x \notin \alpha_i)$ is not the negation of : $\forall i (i \in I \Rightarrow x \in α_i)$, and neither of : $\forall i (x \in α_i)$.