6

$$S=\sum\limits_{i=1}^{4}\tan^{-1} x_i$$

How to simplify this ?

I think I will have to use this :

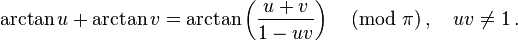
formula

but it looks too long a method .

Is there a method or symmetrical way which yields the answer quickly ?

note : $x_i$ are the roots of a fourth degree polynomial so I know the sum and product of the roots

Community
  • 1
Klosew
  • 713

1 Answers1

2

$S$ is an argument of the complex number $(1+ix_1)(1+ix_2)(1+ix_3)(1+ix_4)$, and if you expand this, you can use what you know about $\sum x_i$ and $\prod x_i$ to simplify it a little.

Hans Lundmark
  • 53,395
  • Scrap of a little in the end . It simplifies everything :) – Klosew Mar 18 '15 at 11:33
  • OK, fine! I didn't actually try to finish the computation, so I didn't know how well it would work. But if you're happy, I'm happy. :-) – Hans Lundmark Mar 18 '15 at 11:46
  • I wonder how this idea came to you ? Is it from expeprience ? – Klosew Mar 18 '15 at 11:48
  • 1
    Yes. :-) When I see $\arctan x$, I always think of a right triangle with sides $1$ and $x$, and also of the complex number $1+ix$, since it is a basic property of complex numbers that multiplication means multiplying their absolute values and adding their arguments. – Hans Lundmark Mar 18 '15 at 13:34
  • 1
    By the way, if one thinks about it, it's pretty clear that this approach should solve the whole problem, since if your polynomial is $p(z)=c(z-x_1)(z-x_2)(z-x_3)(z-x_4)$, then $p(i)$ equals $ci^4$ times your product! – Hans Lundmark Mar 18 '15 at 13:39