Question as the title showed,in which J means Bessel functions, n and m are positive integers. How to get the analytic result? Any comment is much appreciated. Many thanks in advance.How to simplify the following formula when $n>2m+1$ and $n$ is odd.
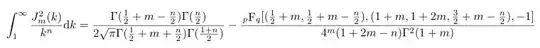
Asked
Active
Viewed 281 times
3
Peng
- 161
-
All results to integrals of this kind are in terms of hypergeometric functions. – Lucian Mar 22 '15 at 11:18
-
@Lucian Will you give the expression as hypergeometric functions? – Peng Mar 22 '15 at 11:29
-
Certainly. – Lucian Mar 22 '15 at 12:30
-
@Lucian May I have the details when Bessels in different order, like $J_n(k) J_{n+1}(k)$? – Peng Mar 23 '15 at 00:29
-
Are you asking me to evaluate $~\displaystyle\int_1^\infty\frac{J_a(k)~J_b(k)}{k^m}~dk~$ in closed form ? – Lucian Mar 23 '15 at 05:18
-
If so, then the answer can be found here. – Lucian Mar 23 '15 at 05:47
-
@Lucian how to simplify the following when $n>2m+1$ and $n$ is odd. – Peng Mar 25 '15 at 02:36
-
I don't think that there are any substantial simplifications to be made. – Lucian Mar 25 '15 at 08:01
-
@Lucian While when I program to compute this, how to handle the case when n>2m+1 and n is odd? – Peng Mar 26 '15 at 01:38
-
Again, I'm not quite sure what's there to “handle”. What precisely is it that seems to be troubling you ? – Lucian Mar 26 '15 at 02:20
-
@Lucian If n=2m+3, $\Gamma(1/2+m-n/2)=\Gamma(-1)$, how to do with $\Gamma(-1)$? – Peng Mar 26 '15 at 04:30
-
In that particular case, we are dealing with an indeterminate expression of the form $\infty-\infty$, but, by taking the limit as $n\to2m+3$, we obtain this result. – Lucian Mar 26 '15 at 10:57
-
@Lucian Excuse me, but I can not link to this result. – Peng Mar 26 '15 at 12:33
-
@Lucian Thank you very much. Which software do you use to compute it? Would you like to show me if n>2m+1 and an odd, namely, n=2m+2s+1 with s positive integer? – Peng Mar 27 '15 at 02:28
-
@Lucian Would you mind showing me detailed derivation? – Peng Mar 28 '15 at 06:55
-
Uhm, no, I wouldn't mind, but, unfortunately I don't possess one... :-$)$ It was the computer that evaluated the expression, not me... :-$)$ – Lucian Mar 28 '15 at 10:25
-
@Lucian Which math software do you use to compute? – Peng Mar 28 '15 at 11:50
-
I use Mathematica and Maple. – Lucian Mar 28 '15 at 11:52
-
@Lucian Would you like to show me if n>2m+1 and an odd, namely, n=2m+2s+1 with s positive integer? – Peng Mar 28 '15 at 11:58
-
@Lucian I am not very familiar with those two software. – Peng Mar 28 '15 at 11:58
-
The same formula holds for all positive values of n. – Lucian Mar 28 '15 at 12:07
-
@Lucian Which formula do you mean? I want a genernal formula that can be used for programming. – Peng Mar 28 '15 at 12:15
-
The one you already posted in the body of your own question. – Lucian Mar 28 '15 at 12:28
-
@Lucian But i can not use that to program as I said $\Gamma(-N)=\infty$ – Peng Mar 28 '15 at 12:39
-
Unfortunately, as I've already said, answering your question would require applying l'Hopital's rule to the entire expression, which will ultimately lead to handling derivatives of hypergeometric functions, with which I personally am extremely unfamiliar, so I'm afraid I can't be of any further help. – Lucian Mar 28 '15 at 14:35