6

Why is

$$\sum_{k=1}^n \log k \ge \int_1^n \log x \, dx$$

is there an intuitive or graphical way to think about it?

Michael Hardy
  • 1
larrysummersstatistics
  • 803
  • 1
    If you write \text{log } instead of \log, then proper spacing does not appear between "log" and what precedes it unless it is added manually, just as you added in manually after log. With \log the spacing is automatically included or not depending on whether it's in a context in which that is appropriate. It is standard usage, and I changed it. ${}\qquad{}$ – Michael Hardy Mar 30 '15 at 03:05
  • Note that $D^{2} \log x < 0$ for $x > 0.$ – Yes Mar 30 '15 at 03:11

3 Answers3

3

Hint 1: $\int_1^n \log x \, dx =\sum_{k=2}^n \int_{k-1}^k \log x \, dx $

Hint 2: If $x \in [k-1,k]$ then $\log(x) \leq \log(k)$.

N. S.
  • 132,525
2

Consider that $\log(x)$ is an increasing function and that $\log(1)=0$, then look at the following plot:

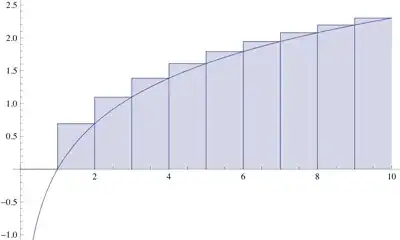
enter image description here

Normally, if $f(x)$ is an increasing function, then, for $a,b\in\mathbb{Z}$, $$ \sum_{k=a+1}^bf(k)\ge\int_a^bf(x)\,\mathrm{d}x $$ but since $f(a)=\log(1)=0$, we can include $1$ in the summation.

robjohn
  • 345,667
1

Draw a picture of $\log x$ and the left and right Riemann sums corresponding to the integral with interval width $1$. Which one matches the sum on the left hand side?

Batman
  • 19,390