I'm asked to show that the Julia set of the function $f(z)=z^2-6$ is a Cantor set contained in $[-3,-\sqrt{3}]\cup [\sqrt{3},3]$. I have identified $3$ as a fixed point of $f$, and found that $-3,-\sqrt{3}, \sqrt{3}$ are bounded components of the Fatou set, i.e., their iterates are bounded (by 3). (Level: basic complex dynamics)
Asked
Active
Viewed 737 times
1 Answers
4
The points $\pm 3$ and $\pm \sqrt{3}$ are in fact in the Julia set... for a polynomial, the Julia set is the boundary of the basin of $\infty$, which is the open set that consists of all points that escape to $\infty$ under iteration. Another way to see this: $3$ is a repelling fixed point, and the others are in its backward orbit.
The story of dynamics on the real line is told by this picture, where the red lines $y=\pm 3$ intersect the parabola $y=x^3-6$ at $\pm \sqrt{3}$ and $\pm 3$.
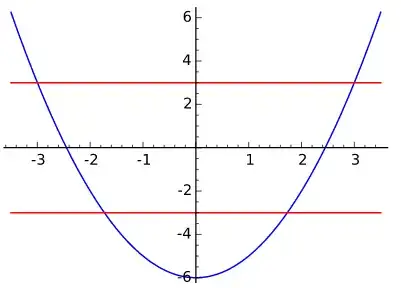
Once a point lands outside of the interval $[-3,3]$, its orbit escapes to infinity. So, the points that do not escape are contained in the intersection $$ [-3,3]\cap f^{-1}([-3,3])\cap f^{-2}([-3,3])\cap \dots $$ which is how the Cantor set is formed: at every step, each connected component loses a piece in the middle, the one that's mapped to $[-\sqrt{3},\sqrt{3}]$.
It remains to show that each point $x_0+iy_0$ with $y_0\ne 0$ escapes to $\infty$ under iteration. Since $|z^2-6|\ge |z|^2-6$, the comparison with the real case shows that every point $z$ with $|z|>3$ escapes (modulus grows). So, if a point of the orbit $z_n=x_n+iy_n$ satisfies $|x_n|\le 1$ for some $n$, then $$\operatorname{Re}( (x_n+iy_n)^2-6) = x_n^2-y_n^2-6 \le -5$$ hence the orbit escapes. But if $|x_n|>1$ for all $n$, then $$|y_{n+1}|=|\operatorname{Im}( (x_n+iy_n)^2-6)| =| 2x_ny_n|>2|y_n|$$ hence $|y_n|\to\infty$.