0

This is similar to this question. What's different is that only the coordinates of the North-East and South-West (or North-West and South-East) corners are known.

My question is, can you directly determine if a point lies inside the rectangle without finding the coordinates of the other 2 corners?

If finding the other 2 coordinates is necessary, what would be a good approach for finding them?

Community
  • 1
κροκς
  • 103

1 Answers1

2

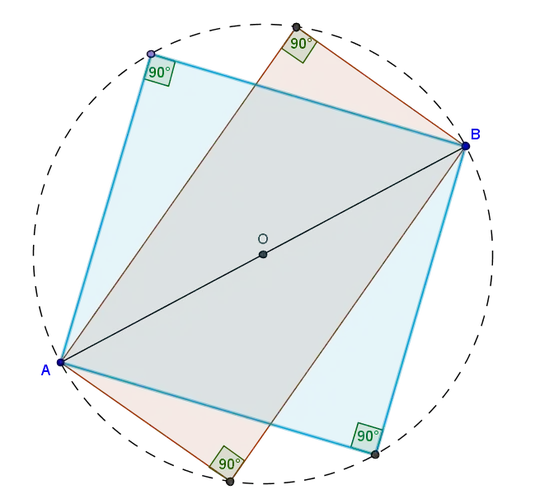
I assume that, as in the question you linked to, the rectangle can have any orientation and is not limited to horizontal/vertical sides.

There are infinitely many rectangles that have two given points as opposite vertices: a third vertex can be any point on the circle that has those two points as the ends of a diameter. A point outside that circle will be in none of the rectangles, while a point on the line segment between the two points will be in all the rectangles. All other points inside the circle but not on the line segment will be in some rectangles and not in others.

Therefore, there is no way to " directly determine if a point lies inside the rectangle without finding the coordinates of the other 2 corners" for those points. Also, there is no way to find the other two corners without additional information.

enter image description here

Rory Daulton
  • 32,288
  • Hi Rory, thanks for the answer! – κροκς Apr 05 '15 at 10:47
  • @kgiou: Yes, that's the point of the circle with the two given points as endpoints of a diameter. Any vertex on that circle is guaranteed to be at a right angle. When a third vertex is chosen on that circle, the fourth vertex is chosen to be immediately opposite it on the circle. When the four vertices are chosen that way, the quadrilateral formed is definitely a rectangle. – Rory Daulton Apr 05 '15 at 10:49