We should take care of the case $\cos(x) = 0$ separately: when $\cos(x) = 0$, $\sin(x) = \pm 1$, and $0^1 = 0$ while $0^{-1}$ is undefined; neither are $1$, so no solutions there.
You do have $\cos(x)^{\sin(x)} = (\pm 1)^0 = 1$ when $x = n \pi$.
Otherwise, if you're interested in real solutions, you have $0 < |\cos(x)| < 1$ and either $\sin(x) > 0$ or $\sin(x) < 0$. If $\sin(x) > 0$, $\left|\cos(x)^{\sin(x)}\right| = |\cos(x)|^{\sin(x)} < 1$, and if $\sin(x) < 0$,
$\left|\cos(x)^{\sin(x)}\right| = |\cos(x)|^{\sin(x)} > 1$, so no more solutions there.
However there can be complex solutions.
By definition, $\cos(x)^{\sin(x)} = \exp(\sin(x) \ln(\cos(x)))$. Note that this can involve the logarithm of negative numbers: that's OK if you allow complex values. If you're not comfortable with complex numbers, don't even consider non-integer powers of negative numbers.
Now $1 = \exp(0)$, so you have solutions when $\sin(x) \ln(\cos(x)) = 0$. This would mean either $\sin(x) = 0$ (which happens when $x = n \pi$ for integer $n$) or $\ln(\cos(x)) = 0$ (which means $\cos(x) = 1$, and that's included in the previous solutions).
However, the complex logarithm is multi-valued, so there are other cases to consider.
$1 = \exp(z)$ for $z = 2 \pi i m$ for integer $m$, so you want to consider $\sin(x) \ln(\cos(x)) = 2 \pi i m$.
Now if $x = it$ is imaginary, $\cos(x) = \cosh(t)$ and $\sin(x) = i \sinh(t)$, so you're looking at $\sinh(t) \ln (\cosh(t)) = 2 \pi m$.
The graph of $\sinh(t) \ln(\cosh(t))$ looks like this:
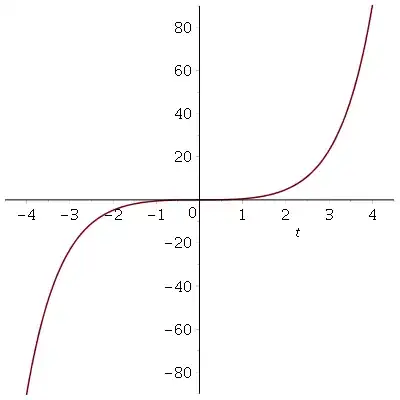
so there should be one solution with real $t$ for every $m$. It probably doesn't have
a closed form, but can be obtained numerically. For $m = 1, 2, 3$ the
solutions are approximately $t = 2.155448920$, $2.587822150$, $2.858727129$ respectively.
There are also lots of solutions with both real and imaginary parts nonzero, e.g.
(approximately) $$ \pm 2.03750688737218 \pm 1.68500078184922 i$$.
Here are all the solutions that I've found using Maple in the rectangle $\{x+iy: -\pi \le x \le \pi, -5 \le y \le 5\}$:
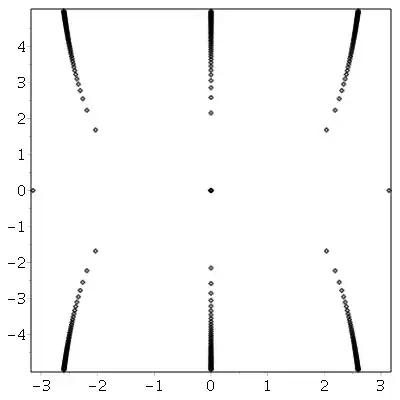
Note that since $\cos$ and $\sin$ are periodic with period $2\pi$, this picture repeats horizontally.

