3

I am learning some basic idea on generating cauchy distribution from uniform random generator $u \in [0, 1]$. I know it was discussed before in How to generate a Cauchy random variable, but during my realization in matlab, I still don't understand how to interpret the results. Here is my matlab code

gam = 10; 
x0 = 0;
u=rand(1,1000);
r = x0 + gam.*tan(pi*(u-0.5));
hist(r);

x = -1000:0.01:1000;
y = (1/pi)*(gam./(gam^2+(x-x0).^2));
plot(x, y);

I got the result from the hist(r) as

enter image description here

However, in second part of code where I plot the actual Cauchy distribution, I saw a very different shape as the first figure. Am I missing anything here?

enter image description here

Community
  • 1
user1285419
  • 397
  • You have run the simulation more than once, changed the bin widths, and so on, right? – Chappers May 03 '15 at 02:21
  • Sorry that I just started and I don't get your question. But I have prepared 1000 samples, each followed into [0, 1] as uniform random distribution. – user1285419 May 03 '15 at 02:25
  • You should probably set your bins manually rather than letting MATLAB do it in the default manner. For instance you might have a single bin for everything less than -1000, a single bin for everything greater than 1000, and 20 bins for things between -1000 and 1000. – Ian May 03 '15 at 02:38

2 Answers2

1

First, as others have mentioned, you're using the default settings for the hist function. As stated right at the beginning of the documentation, this uses 10 equally-spaced bins by default. Try increasing the number:

gam = 10; 
x0 = 0;
u = rand(1,1e4);
r = x0 + gam.*tan(pi*(u-0.5));
hist(r,1e3);
axis([-2000 2000 0 1e4]);

The vertical (dependent) axis is in terms of bin counts as this is a histogram, not a probability density function (PDF) plot. However, just being able to specify the number of bins is not very flexible. This one of several reasons why The MathWorks discourages the use of hist and the underlying histc in current versions of Matlab.

A better, more-flexible alternative is the histogram function, which does a better job of automatic binning even without specifying any additional settings. Additionally, it has options for easily normalizing the histogram as if it were a PDF, if that's what you're after

gam = 10; 
x0 = 0;
u = rand(1,1e4);
r = x0 + gam.*tan(pi*(u-0.5));
edges = -200:10:200;
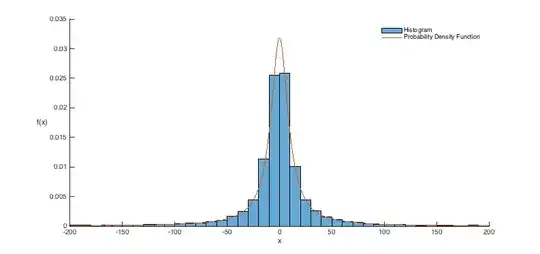
histogram(r,edges,'Normalization','pdf');
hold on;
x = -200:0.01:200;
y = (1/pi)*(gam./(gam^2+(x-x0).^2));
plot(x,y);
axis([x(1) x(end) 0 1.1*max(y)]);

This produces a plot like this: histogram plot


Lastly, you can use kernel density estimation via Matlab's ksdensity function:

gam = 10; 
x0 = 0;
u = rand(1,1e3);
r = x0 + gam.*tan(pi*(u-0.5));
x = -200:0.01:200;
y = (1/pi)*(gam./(gam^2+(x-x0).^2));
f = ksdensity(r,x);
plot(x,y,'r--',x,f,'b');
axis([x(1) x(end) 0 1.1*max(y)]);

which yields a plot something like this:

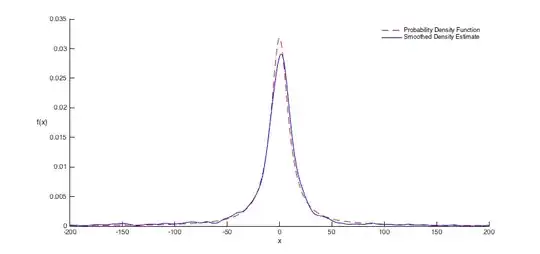
ksdensity plot

More random samples will result in smoother estimates that match your PDF more closely. Be sure to read through the documentation for ksdensity.

horchler
  • 3,203
0

Try to limit the range of your histogram. There are a small number of very extreme values in your Cauchy random sample that are causing the histogram to extend over a very large range, and at the same time causing almost all values to occupy one bin. Notice the density plot ranges only from -1000 to 1000. If you impose a similar range on your histogram (even better, make both plots run from -200 to 200), you won't have almost all your values living in one histogram bin, and the shape of the histogram will become more apparent.

Community
  • 1
grand_chat
  • 38,951
  • I am trying to limit the range to be -100 to 100, in hisstogram, I still see a uniform distribution but in the real plot, I saw the big different plot. – user1285419 May 03 '15 at 02:28
  • What's the problem with generating a row vector of random numbers instead of a column vector of random numbers? – Ian May 03 '15 at 02:35
  • @Ian: You are right, I am misunderstanding the meaning of the arguments. – grand_chat May 03 '15 at 02:38
  • So instead of using hist in matlab, any better way to show the distribution? – user1285419 May 03 '15 at 02:44
  • Oh, I think I see your point now, I am trying to increase the number of bins in the hist and it looks better now. One more question, if I use formula $y = x_0 + \gammatan(\pi(u-0.5))$ where $u$ is the random variable generated by uniform distribution, so is $y$ be the random variable but satisfying Cauchy distribution? – user1285419 May 03 '15 at 02:52
  • Yes, if $y$ is defined as in your formula, then $y$ will satisfy the Cauchy distribution. – grand_chat May 03 '15 at 03:01