2

Given three iid random variables, $X,Y,Z$ following a Uniform $(0,1)$ distribution. Then, how to find $\Pr(X>YZ)$?

Recently, I was asked this question in an interview, but I chocked there. Any hint will be appreciated.

hola
  • 1,339
  • I found the distribution of $YZ$, then tried to find the distribution of $YZ-X$ by convolution, but had trouble coming up with the bounds. Perhaps there is an easier solution. – Math1000 May 09 '15 at 15:47
  • 5
    This has been asked before on the site. The shortest solution uses the fact that, for every $x$ in $(0,1)$, $P(X>x)=1-x$, and the fact that $YZ$ is in $(0,1)$ almost surely. Thus, $$P(X>YZ)=E(1-YZ)=1-E(Y)E(Z)=1-\tfrac12\cdot\tfrac12=\tfrac34.$$ Likewise, for every $n\geqslant1$, with obvious notations, $$P(X>X_1\cdots X_n)=1-\left(\tfrac12\right)^n.$$ – Did May 09 '15 at 18:58
  • @Did One thing is not clear: why $\Pr(X>x)=E(1-x)$? – hola May 09 '15 at 19:07
  • Please read: $P(X>x)=1-x$ for $x$ in $(0,1)$ (not $P(X>x)=E(1-x)$). Well, this seems to be the very definition of the distribution of $X$, no? – Did May 09 '15 at 19:10
  • @Did This is clear, but then where does the expectation come from? – hola May 09 '15 at 19:13
  • 1
    From the fact that one uses this identity as $P(X>YZ\mid Y,Z)=1-YZ$, hence $P(X>YZ)=E(P(X>YZ\mid Y,Z))=E(1-YZ)$. – Did May 09 '15 at 19:16
  • https://math.stackexchange.com/q/1060365/321264 – StubbornAtom May 26 '20 at 19:50

1 Answers1

2

The problem amounts to finding the right range over which to integrate the joint density function to satisfy the inequality $x\gt yz$. Firstly, $x$ can range from $0$ to $1$. Then for a given $x$, the $y,z$ satisfying $yz\lt x$ is shown by the shaded region of the diagram.

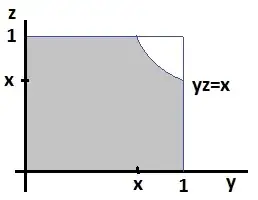
enter image description here

So we need to integrate in two pieces:

\begin{eqnarray*} P(X\gt YZ) &=& \int_{x=0}^1 \int_{y=0}^x \int_{z=0}^1 1\;dz\;dy\;dx + \int_{x=0}^1 \int_{y=x}^1 \int_{z=0}^{x/y} 1\;dz\;dy\;dx \\ &=& \int_{x=0}^1 \int_{y=0}^x 1\;dy\;dx + \int_{x=0}^1 \int_{y=x}^1 \dfrac{x}{y}\;dy\;dx \\ &=& \int_{x=0}^1 x\;dx + \int_{x=0}^1 \left[ x\ln{y} \right]_x^1\;dx \\ &=& \int_{x=0}^1 x\;dx - \int_{x=0}^1 x\ln{x} \;dx \\ &=& \left[\dfrac{1}{4}x^2(3-2\ln{x})\right]_0^1 \\ &=& \dfrac{3}{4}.\end{eqnarray*}

Mick A
  • 10,208