I know these equations are called general equation of second degree and also represent a pair of straight lines. I could extract lines from the equation $$12x^2+7xy-12y^2 =0 $$ (these are $$ 3x+4y=0$$ and $$4x-3y=0$$) but I don't know how to separate lines from $$12x^2+7xy-12y^2-x+7y-1=0.$$ I think we have to find the solution by finding out the difference between all four straight lines but I have trouble separating them. Thank you!
-
1Hint: consider the expression as a quadratic equation in $x$ and try to factor it. – Jef May 25 '15 at 17:12
-
$(3x+4y-1)(4x-3y+1)$. – André Nicolas May 25 '15 at 17:14
-
I did but how did -1 and +1 come at the end ? – Seeker1201 May 25 '15 at 17:27
-
Well, you can check that they work. The constant term at the end of your expression is $-1$. There are not many ways to factor it as a product of integers, just $(-1)(1)$ and $(1)(-1)$. Of course it could have been factions, or something worse, but that would likely not produce integer coefficients in the product. – André Nicolas May 25 '15 at 17:30
-
@Nancy: The constant term in the quadratic in $x$ is $-12y^2+7y-1$, which itself factors to $(4y-1)(-3y+1)$. So you could say the $\pm1$'s came from the $-1$ and $+1$, or that they are just part if the binomials in $y$. – Rory Daulton May 25 '15 at 17:31
-
So, we have to factor the quadratic equation like we normally do and add - constant term and +constant term at the end ? But then how will I determine that in which equation do i have to add and subtract the constant term ? – Seeker1201 May 25 '15 at 17:39
-
there is a discussion of the "center" of a conic section at http://math.stackexchange.com/questions/1286146/how-to-find-center-of-a-conic-section-from-the-equation – Will Jagy May 25 '15 at 18:05
-
Let's see: in your second equation, the center is at $(-1/25, 7/25).$ This gives asymptotic lines $3x+4y = 1,$ $4x-3y= -1,$ and the curve(s) becomes $$ (3x+4y-1)(4x-3y+1) = \rm{something}. $$ In your second equation, that something becomes $0.$ If your second equation were altered to $12x^2+7xy-12y^2-x+7y=0,$ you would instead have the *hyperbola* $$ (3x+4y-1)(4x-3y+1) = -1. $$ Try to graph that on graph paper, I suggest five squares per inch http://www.printablepaper.net/category/graph and five: http://www.printablepaper.net/preview/grid-portrait-letter-5-index – Will Jagy May 25 '15 at 18:36
3 Answers
In order to avoid the cumbersome calculations, assume that the lines are: $y=m_{1}x+c_{1}$ & $y=m_{2}x+c_{2}$ Now, the quadratic equation of pair of the lines is given as
$$(m_{1}x-y+c_{1})(m_{2}x-y+c_{2})=0 $$$$\implies m_{1}m_{2}x^2-(m_{1}+m_{2})xy+y^2+(m_{1}c_{2}+m_{2}c_{1})x-(c_{1}+c_{2})y+c_{1}c_{2}=0 \tag 1$$ The given equation of pair of lines : $12x^2+7xy-12y^2-x+7y-1=0$ can be written as
$$-x^2-\frac{7}{12}xy+y^2+\frac{1}{12}x-\frac{7}{12}y+\frac{1}{12}=0 \tag 2$$ Now, compare both the above equations (1) & (2), we have $$m_{1}m_{2}=-1 \quad \text{&} \quad m_{1}+m_{2}=\frac{7}{12} \tag 3$$$$ \implies m_{1}-m_{2}=\sqrt{(m_{1}+m_{2})^2-4m_{1}m_{2}}=\sqrt{\left(\frac{7}{12}\right)^2-4(-1)}=\frac{25}{12}\tag 4$$
(Note: $m_{1}$ & $m_{2}$ are unknown hence, their signs will be automatically decided after calculation)
Now, Solving the equations (3) & (4), we get $$m_{1}=\frac{4}{3} \quad \text{&} \quad m_{2}=-\frac{3}{4}$$ Similarly, by comparing the above equations (1) & (2), we have $$c_{1}c_{2}=\frac{1}{12} \quad \text{&} \quad c_{1}+c_{2}=\frac{7}{12} \tag 5$$$$ \implies c_{1}-c_{2}=\sqrt{(c_{1}+c_{2})^2-4c_{1}c_{2}}=\sqrt{\left(\frac{7}{12}\right)^2-4\left(\frac{1}{12}\right)}=\frac{1}{12}\tag 6$$ (Note: $c_{1}$ & $c_{2}$ are unknown hence, their signs will be automatically decided after calculationc)
Now, Solving the equations (5) & (6), we get $$c_{1}=\frac{1}{3} \quad \text{&} \quad c_{2}=\frac{1}{4}$$ Hence, by setting the corresponding values, we get the equations of the lines as follows $$y=\frac{4}{3}x+\frac{1}{3} \quad \text{&} \quad y=-\frac{3}{4}x+\frac{1}{4}$$ $$\implies 4x-3y+1=0 \quad \text{&} \quad 3x+4y-1=0$$
- 37,450
As I wrote in comment, your second equation does come out to two lines, as everyone pointed out. If we slightly alter it we get a hyperbola , $$ 12 x^2 + 7 xy - 12 y^2 - x + 7 y = 0, $$ which passes through the origin and is asymptotic to your two shifted lines, which now cross each other at $(-1/25, 7/25)$
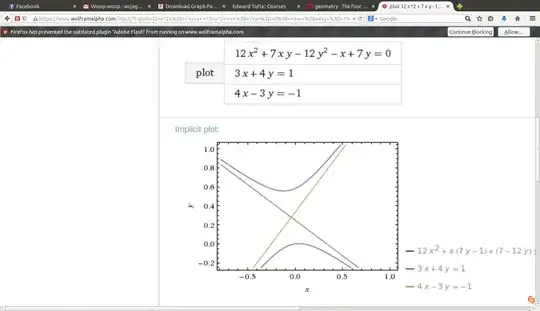 Here it is including the $x,y$ axes
Here it is including the $x,y$ axes

If we alter the constant in the other direction, we get a different hyperbola but still asymptotic to those lines,
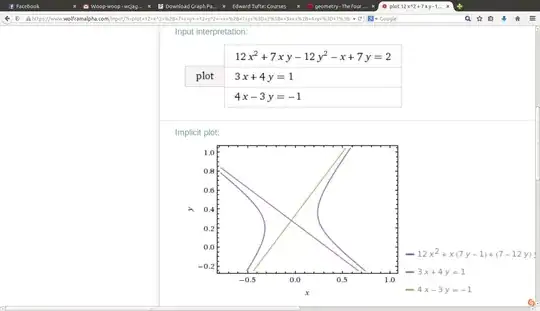 Here is this one with axes
Here is this one with axes
- 139,541
For large $x$ and $y$, the equation approaches $$12x^2+7xy-12y^2-x+7y-1\approx 12x^2+7xy-12y^2 = (3x+4y)(4x-3y)$$ Then, write
$$12x^2+7xy-12y^2-x+7y-1= (3x+4y+a)(4x-3y+b)$$
Solve to obtain $a=-b=-1$.
- 97,352