3

$n!>(\frac{n}{e})^n$

$$(n+1)!=n!(n+1)>(\frac{n}{e})^n(n+1)=(\frac{n+1}{e})^{n+1}\times \frac{(\frac{n}{e})^n(n+1)}{(\frac{n+1}{e})^{n+1}}>(\frac{n+1}{e})^{n+1}$$ This implies, but I think $$\frac{(\frac{n}{e})^n(n+1)}{(\frac{n+1}{e})^{n+1}}$$ should be considered further (more induction steps)

$n!<e(\frac{n}{2})^n$

$$n!(n+1)<e(\frac{n}{2})^n(n+1)=e(\frac{n}{2})^n(n+1)\times \frac{(\frac{n+1}{2})^{n+1}} {(\frac{n+1}{2})^{n+1}}<e(\frac{n+1}{2})^{n+1}$$ Also, $$\frac{e(\frac{n}{2})^n(n+1)}{(\frac{n+1}{2})^{n+1}}$$ I think more steps are needed.

Can someone check this and tell if something is missing.

Martin Sleziak
  • 53,687
user300045
  • 3,449

2 Answers2

1

We know that $\lim_{n\to\infty}\left(1+\frac 1n\right)^n=e$ and that $\left(1+\frac 1n\right)^n$ is increasing (see, for example, here), so we have for $n\ge 2$ $$e\gt \left(1+\frac 1n\right)^n\gt 2,$$ i.e. $$\left(\frac ne\right)^n\cdot(n+1)\gt \left(\frac{n+1}{e}\right)^{n+1}\ \ \ \ \ \text{and}\ \ \ \ \ e\left(\frac n2\right)^n\cdot(n+1)\lt e\left(\frac{n+1}{2}\right)^{n+1}.$$

Community
  • 1
mathlove
  • 139,939
1

I had originally written this up for another question but it seems fitting here as well. Maybe this can help someone.

Depending on how you introduced $e$, you might be able to use the fact that there are two sequences $(a_n)_{n \in \mathbb{N}}$, $(b_n)_{n \in \mathbb{N}}$ with

$$\begin{align} a_n ~~~&:=~~~ \left ( 1 + \frac{1}{n} \right ) ^n \\ ~ \\ b_n ~~~&:=~~~ \left ( 1 - \frac{1}{n} \right ) ^{-n} \end{align}$$

and

$$\underset{n \rightarrow \infty}{\lim} a_n ~~~=~~~ \underset{n \rightarrow \infty}{\lim} b_n ~~~=~~~ e \\ ~ \\$$

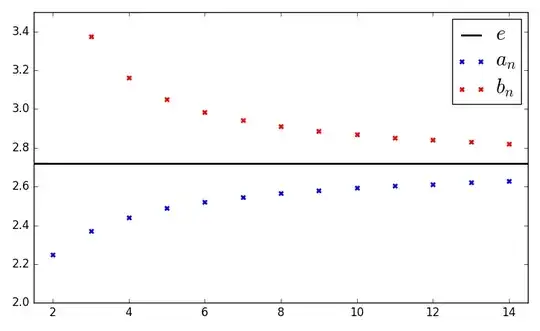
While both sequences converge to the same limit, $a_n$ approaches from the bottom and $b_n$ approaches from the top:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams.update({'figure.autolayout': True})

pts = np.arange(0, 20, 1)
a_n = lambda n: (1+1/n)**n
b_n = lambda n: (1-1/n)**(-n)

plt.errorbar(x = pts, xerr = None, y = a_n(pts), yerr = None, fmt = "bx", markersize = "5", markeredgewidth = "2", label = "$a_n$")
plt.errorbar(x = pts, xerr = None, y = b_n(pts), yerr = None, fmt = "rx", markersize = "5", markeredgewidth = "2", label = "$b_n$")
plt.plot(pts, [np.exp(1)]*len(pts), color = "black", linewidth = 2, label = "$e$")
plt.xlim(1.5, 14.5)
plt.ylim(2.0, 3.5)
plt.legend(loc = "best")
plt.setp(plt.gca().get_legend().get_texts(), fontsize = "22")
plt.show()

So we're going to use the following inequality:

$$\forall n \in \mathbb{N} ~ : ~~~~~ \left ( 1 + \frac{1}{n} \right ) ^n ~~~~<~~~~ e ~~~~<~~~~ \left ( 1 - \frac{1}{n} \right ) ^{-n} \tag*{$\circledast$} \\ ~ \\$$

Thesis

$$\forall n \in \mathbb{N}, ~ n \geq 2 ~ : ~~~~~ e \cdot \left ( \frac{n}{e} \right )^n ~~~~<~~~~ n! ~~~~<~~~~ n \cdot e \cdot \left ( \frac{n}{e} \right )^n \\ ~ \\$$

Proof By Induction

Base Case

We begin with $n = 2$ and get

$$\begin{align} & ~ && e \cdot \left ( \frac{2}{e} \right )^2 ~~~~&&<~~~~ 2! ~~~~&&<~~~~ 2 \cdot e \cdot \left ( \frac{2}{e} \right )^2 \\ ~ \\ & \Leftrightarrow && e \cdot \frac{4}{e^2} ~~~~&&<~~~~ 1 \cdot 2 ~~~~&&<~~~~ 2 \cdot e \cdot \frac{4}{e^2} \\ ~ \\ & \Leftrightarrow && \frac{4}{e} ~~~~&&<~~~~ 2 ~~~~&&<~~~~ \frac{8}{e} \\ ~ \\ &\Leftrightarrow && 2 ~~~~&&<~~~~ e ~~~~&&<~~~~ 4 ~~~~ \\ \end{align} $$

Which is a true statement.

Inductive Hypothesis

Therefore the statement holds for some $n$. $\tag*{$\text{I.H.}$}$

Inductive Step

$$\begin{align} & ~ && e \cdot \left ( \frac{n+1}{e} \right )^{n+1} \\ ~ \\ & = && (n+1) \cdot \frac{1}{e} \cdot e \cdot \left ( \frac{n+1}{e} \right )^n\\ ~ \\ & = && (n+1) \cdot \left ( \frac{n}{e} \right )^n \cdot \left ( \frac{n+1}{n} \right )^n\\ ~ \\ & = && (n+1) \cdot \left ( \frac{n}{e} \right )^n \cdot \left ( 1 + \frac{1}{n} \right )^n\\ ~ \\ & \overset{\circledast}{<} && (n+1) \cdot \left ( \frac{n}{e} \right )^n \cdot e\\ ~ \\ & \overset{\text{I.H.}}{<} && (n+1) \cdot n!\\ ~ \\ & = && (n+1)!\\ ~ \\ & = && (n+1) \cdot n!\\ ~ \\ & \overset{\text{I.H.}}{<} && (n+1) \cdot n \cdot e \cdot \left ( \frac{n}{e} \right )^n\\ ~ \\ & = && (n+1) \cdot e \cdot \left ( \frac{n}{e} \right )^{n+1} \cdot e \\ ~ \\ & = && (n+1) \cdot e \cdot \left ( \frac{n+1}{e} \right )^{n+1} \cdot \left ( \frac{n}{n+1} \right )^{n+1} \cdot e \\ ~ \\ & = && (n+1) \cdot e \cdot \left ( \frac{n+1}{e} \right )^{n+1} \cdot \left ( 1 - \frac{1}{n+1} \right )^{n+1} \cdot e \\ ~ \\ & \overset{\circledast}{<} && (n+1) \cdot e \cdot \left ( \frac{n+1}{e} \right )^{n+1} \cdot \left ( 1 - \frac{1}{n+1} \right )^{n+1} \cdot \left ( 1 - \frac{1}{n+1} \right )^{-(n+1)} \\ ~ \\ & = && (n+1) \cdot e \cdot \left ( \frac{n+1}{e} \right )^{n+1} \\ ~ \\ \end{align} $$

Conclusion

Therefore the statement holds $\forall n \in \mathbb{N}, ~ n \geq 2$. $$\tag*{$\square$}$$

Steph-P
  • 165