0

I need to get from this: $$\sum_{i=1}^n {1\over i(i+1)}$$ to: $${n\over n+1}$$ or: $${1 - {1\over n+1}}$$ I have tried looking for sums identities with fractions, using WolframAlpha.com (that's how I got the results above) and reading my textbook, but I don't get how to manipulate this. Thank you.

edit: What I did:

Based on Idris' answer, I took the sum to be: $${1\over1}-{1\over 1+1}+{1\over 2}-{1\over2+1}+{1\over 3}-{1\over3+1}+...+{1\over n}-{1\over n+1}$$ With that, the groups like $-{1\over 1+1}+{1\over 2}$ cancel each other out (telescoping?) and in the end what's left is: $$1-{1\over n+1}$$ the result that I was looking for! Thank you again, Idris!

Jonas Meyer
  • 53,602
sempiedram
  • 17

3 Answers3

5

HInt: Write $1/i(i+1)=1/i-1/(i+1)$ then the sum telescopes.

UPDATE1: Telescopes, each two neighboring terms cancel, like this $$SUM= [1/1\color{red}{-1/(1+1)}]+[\color{red}{1/2}-1/(2+1)]+....$$ UPDATE 2: https://en.wikipedia.org/wiki/Telescoping_series

Idris Addou
  • 4,193
  • Hmm. "telescopes" is a method I don't know, but thanks, I'll read into that. – sempiedram Jun 16 '15 at 02:15
  • 1
    Telescopes means that terms cancel. Using the partial fraction decomposition the sum is equal to

    $$1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + \cdots$$

     – Simon S Jun 16 '15 at 02:18
  • @sempiedram. You are welcome. You can improve the presentation: instead of one line use two columns (the left one contains the $1/i$ values and the right one contains the $-1/(i+1)$ values, and the cancellation would be in diagonals, its beautiful ! – Idris Addou Jun 16 '15 at 03:20
  • Yes, quite interesting how it works. – sempiedram Jun 16 '15 at 03:53
1

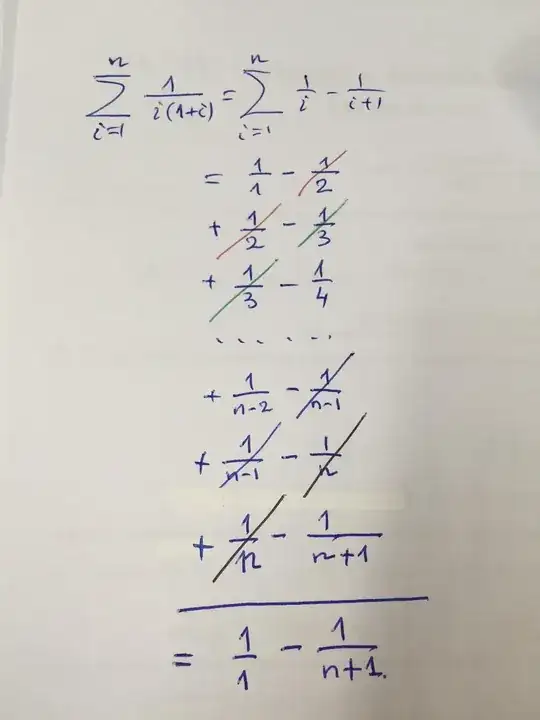Telescoping sum Here is a picture showing the two columns and the cancellations in diagonals

Idris Addou
  • 4,193
0

Another telescope:

$$\begin{align} \sum_{i=1}^{n}\frac 1{i(i+1)}&=\sum_{i=1}^n\left(\frac i{i+1}-\frac{i-1}i\right)\\ &=\frac n{n+1}\qquad\blacksquare \end{align}$$

Hypergeometricx
  • 22,657