To find out the greatest among the number given below:
$3^{1/3}, 2^{1/2}, 6^{1/6}, 1, 7^{1/7}$
I have plotted the following graph using graph plotter which is shown below:
It can be concluded that $3^{1/3}$ is the greatest. I want to know that is there any other method to find greatest among the such numbers.
Take lcm$(3,2,6,7)=42$
We need to check for $3^{1/3},2^{1/2},6^{1/6},7^{1/7}$
equivalently taking $42$nd power of each $3^{14},2^{21},6^7,7^6$
Now $2^3<3^2\iff(2^3)^7<(3^2)^7$
Again, $3^{14}-6^7=3^7(3^7-2^7)>0$
and finally $3^7>3^6=729>343=7^3\implies(3^7)^2>(7^3)^2$
you can also get the result by Algebra: $$3^{1/3}>2^{1/2}$$ powering by $6$ we get $$9>8$$, $$3^{1/3}>6^{1/6}$$ powering by $$6$$ we get $$9>6$$ $$3^{1/3}>1$$ is clear, and $$3^{1/3}>7^{1/7}$$ powering by $21$ gives $$3^7>7^3$$ this is true since $$2187>343$$
Let $f(x)=x^{\frac 1x}$ for $x\gt 0$. Then, we have $$f'(x)=\frac{1-\ln x}{x^2}\cdot x^{\frac 1x}$$ Thus, $f(x)$ is increasing for $0\lt x\lt e$ and is decreasing for $x\gt e$.
So, you only need to compare $f(2)$ with $f(3)$. Now note that $f(3)\gt f(4)=f(2)$.
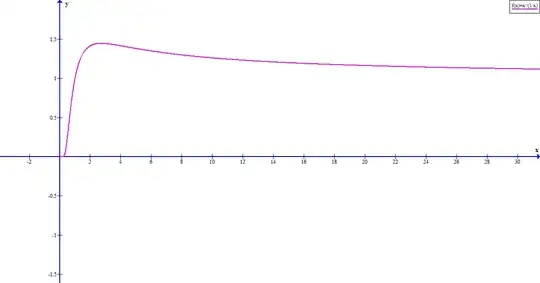
suppose the sequence $a_n=\sqrt[n]{n}$
it is easy to see that $a_n$ converges to $1$
now not that $a_3 $is the biggest
$$a_1=1 ,a_2=\sqrt{2} ,a_3=\sqrt[3]{3} ,a_4=\sqrt[4]{4} ,a_5=\sqrt[5]{5} ,... $$
let's see again :
$$a_1=1 ,{\color{Red} {a_2=\sqrt{2}}} ,a_3=\sqrt[3]{3} ,{\color{Red}{a_4=\sqrt[4]{4}=\sqrt{2}}} ,a_5=\sqrt[5]{5} ,... $$ it means $$1=a_1 <a_2 <{\color{Red} {a_3}} >a_4>a_5 >... \lim_{n \to \infty }\sqrt[n]{n}=1\\because \\a_2=a_4$$
$$a_2>a_1 ,\sqrt{2}=1.41 >1\\a_3>a_2 :\sqrt[3]{3}=\sqrt[6]{3^2} >\sqrt[2]{2}=\sqrt[6]{2^3}\\a_2=a_4$$ until now $a_3$ is greatest
$$a_3 >a_6 :becuase :\sqrt[3]{3}=\sqrt[6]{9} >\sqrt[6]{6}=a_6 $$
$$a_3 >a_7 :becuase :\sqrt[3]{3}=\sqrt[21]{3^7} >\sqrt[21]{7^3}=a_7 $$ it seems $a_3$ is maximum
