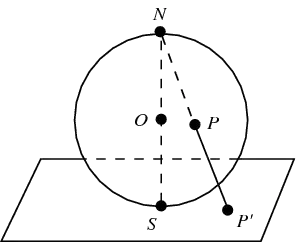
I was working out Gamelin's Complex Analysis and read through the part where he finds an expression for the chordal distance on the Riemann Sphere corresponding to the stereographic projection w.r.t. North Pole $N(0,0,1)$:
$$\phi(u,v,w)=\bigg(\frac{u}{1-w},\frac{v}{1-w}\bigg)$$ $$\phi^{-1}(x,y)=\bigg(\frac{2x}{x^2+y^2+1},\frac{2y}{x^2+y^2+1},\frac{x^2+y^2-1}{x^2+y^2+1}\bigg)$$
He starts with $$\hat{d}(z,w)=|\phi^{-1}(z)-\phi^{-1}(w)|$$ and works out to get an expression $$\hat{d}(z,w)=\frac{2|z-w|}{\sqrt{(1+|z|^2)}\sqrt{(1+|w|^2)}}$$
Everything was fine until I started finding such an expression for stereographic projection of the sphere below:$$x^2+y^2+\bigg(z-\frac12\bigg)^2=\frac14$$
The map turned out to be
$$\psi(u,v,w)=\bigg(\frac{u}{1-w},\frac{v}{1-w}\bigg)$$ $$\psi^{-1}(x,y)=\bigg(\frac{x}{x^2+y^2+1},\frac{y}{x^2+y^2+1},\frac{x^2+y^2}{x^2+y^2+1}\bigg)$$
Then taking
$$\hat{d}(z,w)=|\psi^{-1}(z)-\psi^{-1}(w)|=|x-y|\,\,\,\,\text{(say)}$$
where $\psi^{-1}(z)=x=(x_1,x_2,x_3)$ and $ \psi^{-1}(w)=y=(y_1,y_2,y_3)$
Then$$[\hat{d}(z,w)]^{2}=|x-y|^2=\langle x-y,x-y\rangle=\langle x,x\rangle +\langle y,y\rangle -2\langle x,y\rangle$$
Solving further and substituting values of $x_i$'s and $y_j$'s from the map, i got to the point
$$[\hat{d}(z,w)]^{2}=\frac{|z|^2}{(|z|^2+1)^2}+\frac{|y|^2}{(|y|^2+1)^2}+\frac{2y\bar{z}+2\bar{y}z+|z|^2|y|^2}{2(|z|^2+1)(|y|^2+1)}$$
Any help to proceed further would be appreciated. Thank you.