3

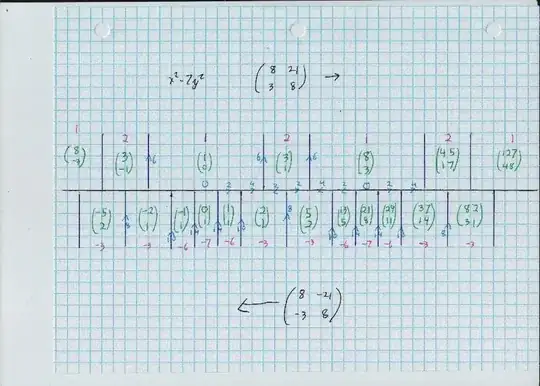
I'd like to solve the following Pell equation: $$ x^2-7y^2=-3 $$ Where $x$ and $y$ are integers. I applied the usual procedure, which avoids continued fractions:

The two minimal positive integer solutions are $(x_0,y_0)=(2,1)$ and $(x_1,y_1)=(5,2)$, thus the minimal rational solution of $x^2-7y^2=1$ should be $(p,q)=\left(\frac{4}{3},\frac{1}{3}\right)$. My script (it is in german so I don't link it here) tells me, that in this case, every pair of solutions is given by: $$ x_{n+1}=\frac{4}{3}x_{n}+7\cdot\frac{1}{3}y_n \\ y_{n+1}=\frac{1}{3}x_{n}+\frac{4}{3}y_n $$ If we proceed further, we can find that this gives: $$ x_n=\frac{a_n}{3^n} \space\text{where}\space a_0=2,\space a_1=15,\space a_{n+1}=8a_n-9a_{n-1} \\ y_n=\frac{b_n}{3^n} \space\text{where}\space b_0=1,\space b_1=6,\space b_{n+1}=8b_n-9b_{n-1} $$ But if we take these equations modulo $9$, we see that $(2,1)$ and $(5,2)$ are the only integer solution, but there surely is also $(37,14)$. Where did I go wrong? Every answer will be appreciated, but I'm not used to the approach with continued fractions, so preferably I would like to see an answer avoiding this.

EDIT:

My main question is:

Where is my fault? Or is my script wrong?

Redundant Aunt
  • 12,030
  • 2
  • 22
  • 66

2 Answers2

5

Don't know about your script. I checked with a Conway topograph, you do have all the necessary "seed" solutions. Also, because we can negate either $x$ or $y$ as wished, we do not need to add in negative solutions. So, given any solution $x^2 - 7 y^2 = -3,$ you get a new solution with $$ (x,y) \mapsto (8x+21y, \; \; 3x+8y). $$ We get two orbits under the oriented automorphism group, $$ (-5,2), $$ $$ (2,1), $$ $$ (37,14), $$ $$ (590,223), $$ $$ (9403,3554), $$ und so weiter. Then $$ (-2,1), $$ $$ (5,2), $$ $$ (82,31), $$ $$ (1307,494), $$ $$ (20830,7873), $$

The other description, for either one of the two strings of solutions, is $$ x_{n+2} = 16 x_{n+1} - x_n, $$ $$ y_{n+2} = 16 y_{n+1} - y_n. $$ For example $16 \cdot 5 - (-2) = 82.$ Or $16 \cdot 82 -5 = 1307.$ Also $16 \cdot 2 -1 = 31$

Here is the diagram, all that is necessary for this problem.

enter image description here

Since I forgot that I had written programs to get the diagram right and correct any arithmetic errors i might make, let me record the relevant part of the output below. The output is the diagram rotated by $90^\circ$

 ./Conway_Topograph_Pointed 1 0 -7 > Conway_1_0_-7.txt


            8   -21           -7    0    1           -3     8
   14
            5   -13           -6    2    1           -3     8
   10
            2    -5           -3    4    1           -3     8
                                                                6
            2    -5           -3   -2    2           -1     3
    8
            1    -2           -3    2    2           -1     3
                                                                6
            1    -2           -3   -4    1            0     1
   10
            1    -1           -6   -2    1            0     1
   14
            1     0           -7    0    1            0     1
   14
            1     1           -6    2    1            0     1
   10
            1     2           -3    4    1            0     1
                                                                6
            1     2           -3   -2    2            1     3
    8
            2     5           -3    2    2            1     3
                                                                6
            2     5           -3   -4    1            3     8
   10
            5    13           -6   -2    1            3     8
   14
            8    21           -7    0    1            3     8

Not really anyone else who goes so far as to draw these diagrams, here are others and books by Conway and Stillwell to explain it

Another quadratic Diophantine equation: How do I proceed?

How to find solutions of $x^2-3y^2=-2$?

Generate solutions of Quadratic Diophantine Equation

Finding all solutions of the Pell-type equation $x^2-5y^2 = -4$

Find all integer solutions for the equation $|5x^2 - y^2| = 4$

Maps of primitive vectors and Conway's river, has anyone built this in SAGE?

Infinitely many systems of $23$ consecutive integers

Small integral representation as $x^2-2y^2$ in Pell's equation

Solving the equation $ x^2-7y^2=-3 $ over integers

http://www.maa.org/press/maa-reviews/the-sensual-quadratic-form (Conway)

http://www.springer.com/gp/book/9780387955872 (Stillwell)

Community
  • 1
Will Jagy
  • 139,541
4

$x^2-7y^2$ is the norm of the quadratic field $\mathbb{Q}(\sqrt{7})$. An element with norm $-3$ in this field is $2+\sqrt{7}$. Then every other solution is different from this solution by a multiplication that has norm $1$. We know that all of the norms are generated by the powers of the primitive solution $8+3 \sqrt{7}$ (I think, check me on this one.) Thus, all of the solutions are $(2+\sqrt{7})(8+3\sqrt{7})^n$ (Obviously, we take the integer part as $x$ and the coefficient of $\sqrt{7}$ as $y$.)

Sandeep Silwal
  • 8,135