1

if n is a positive integer let Z be the subset of integer in {1,...,n} which are relatively prime to n

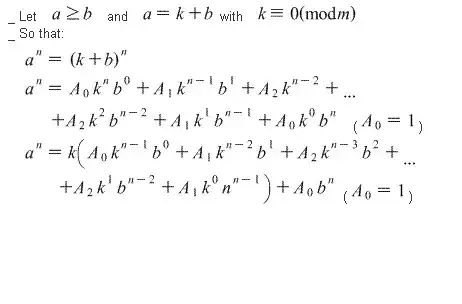
enter image description here

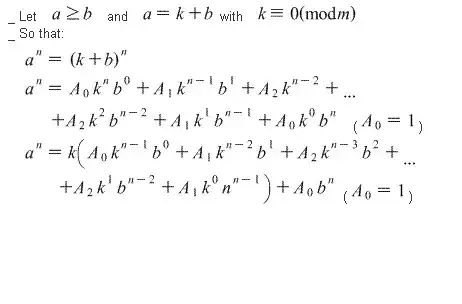
my effort to solve this question enter image description here

I''m confused and need help to solve this question please

user155971
  • 1,515
  • 1
    Your current "solution" doesn't seem to be on the right track. Start with the assumption that $a,b$ are relatively prime to $n$. In GCD notation this is $(a,n)=(b,n)=1$. You're required to show that $(ab,n)=1$ which will imply the result. As a hint, you could write the prime factorization of $a,b$ and $n$ – Alex R. Sep 01 '15 at 18:48

2 Answers2

1

The elements of $\mathbf Z_n^\times$ are the integers in $\{1,\dots,n\}$ which have an inverse modulo $n$ (thanks to Bézout's theorem).

Now if $aa'\equiv 1\mod n$ and $bb'\mod n$, then $(ab)(a'b')=(aa')(bb')\equiv1\mod n$, hence $ab$ has an inverse modulo $n$.

Bernard
  • 175,478
0

You only need to show that if $a,b\in \mathbb{Z}_n^*$, i.e., if $gcd(a,n)=gcd(b,n)=1$, then also $gcd(ab,n)=1$, and hence $ab\in \mathbb{Z}_n^*$. You can find the proof several times here on this site, e.g. here, or here.

Community
  • 1
Dietrich Burde
  • 130,978