I'm looking for a geometrical prove of $$\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$$ and $$\sin(a+b)=\sin(a)\cos(b)+\sin(b)\cos(a)$$ using the trigonometry circle. I tried to search on google, but I didn't find any geometrically proofs of those formulas using the trigonometrical circle.
-
Are you allowed to use complex numbers? Or do you have to use geometrical methods? I would show the geometrical proof but i don't have a proper picture. – MrYouMath Oct 01 '15 at 11:20
-
It looks like you have a nice figure at the Wikipedia https://en.wikipedia.org/wiki/List_of_trigonometric_identities#Angle_sum_and_difference_identities – Miguel Oct 01 '15 at 11:21
-
1http://www.math.wisc.edu/~leili/teaching/math222s11/problems/quizzes/trig.pdf – R.N Oct 01 '15 at 11:21
-
no, only basic geometry – ZiK789 Oct 01 '15 at 11:22
-
1@Narasimham. I guess you meant http://trigonography.com/2015/09/28/angle-sum-and-difference-for-sine-and-cosine/ – Tom-Tom Oct 01 '15 at 12:24
-
1Right, I meant Blue's trigonography. – Narasimham Oct 01 '15 at 12:34
-
Here's something interesting you might not know about. Let $i^2=-1$ (there is no real number with that property but let's ignore that for a bit). Then:$$(\cos a+i\sin a)(\cos b+i\sin b)=\ \cos(a+b)+i\sin(a+b)$$This is equivalent to the sum formulae. – Akiva Weinberger Oct 01 '15 at 15:28
4 Answers
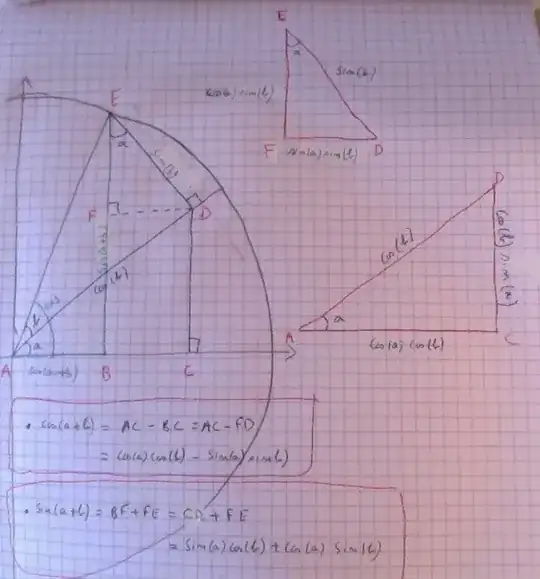
I made this draw. It goes like this:
Draw first the two angles $a$ and $b$ in the trigonometric circle. Project $AE$ on $AD$. Since $|AE|=1$ and that the triangle $ADE$ is rectangle in $D$, you have that $|AD|=\cos(b)$ and $|ED|=\sin(b)$. Now project $AD$ on $AC$, since the triangle $ACD$ is rectangle in $C$ and that $|AD|=\cos(b)$, you have that $|CD|=\cos(b)\sin(a)$ and $|AC|=\cos(a)\cos(b)$. Finally project $ED$ on $EF$. The angle $\hat{FEA}=a$. Moreover, the triangle $EFD$ is rectangle on $F$ and thus $|EF|=\cos(a)\sin(b)$ and $|FD|=\sin(a)\sin(b)$. Now, just remark that $|FB|=|CD|$ and $|BC|=|FD|$ and you get $$\sin(a+b)=|EF|+|FB|=\cos(a)\sin(b)+\sin(a)\cos(b)$$ and $$\cos(a+b)=|AC|-|BC|=\cos(a)\cos(b)-\sin(a)\sin(b).$$
- 55,662
- 7,790
-
-
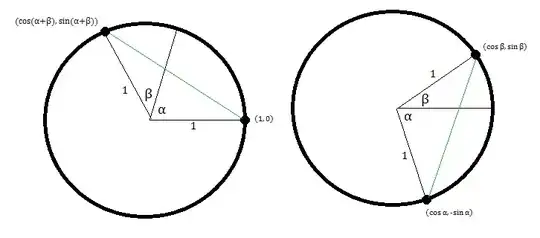
1Nice and simple. Also, if you add a vector at angle $\alpha + \beta + \frac 12 \pi$ and connect that to $(1, 0)$, then you can get the relation for $\sin(\alpha + \beta)$. – DanielV Oct 02 '15 at 00:30
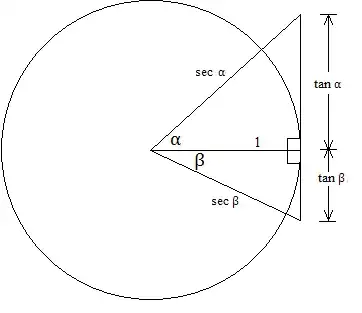
I remember the way that I proved this with acute angles when I was in high school. In looking at the problem, the unit circle seemed to be inviting me to draw right triangles inside of it. Somehow, though, I was able to resist its lure, and instead drew the opposite sides of my triangles tangent to the unit circle.
To find $\sin (\alpha+\beta)$, we use the law of sines and the sine of a compliment identity. $$\begin{array}{lll} \displaystyle\frac{\sin (\alpha+\beta)}{\tan\alpha+\tan\beta}&=&\displaystyle\frac{\sin(\frac{\pi}{2}-\alpha)}{\sec\beta}\\ \sin (\alpha+\beta) &=& \cos\alpha\cos\beta(\tan\alpha+\tan\beta)\\ \sin (\alpha+\beta) &=& \sin\alpha\cos\beta+\cos\alpha\sin\beta\\ \end{array}$$ To find $\cos (\alpha+\beta)$, we use the law of cosines $$\begin{array}{lll} (\tan\alpha+\tan\beta)^2 &=& \sec^2\alpha+\sec^2\beta-2\sec\alpha\sec\beta\cos(\alpha+\beta)\\ \tan^2\alpha+2\tan\alpha\tan\beta+\tan^2\beta&=&\tan^2\alpha+1+\tan^2\beta+1-2\sec\alpha\sec\beta\cos(\alpha+\beta)\\ \tan\alpha\tan\beta&=&1-\sec\alpha\sec\beta\cos(\alpha+\beta)\\ \sec\alpha\sec\beta\cos(\alpha+\beta)&=&1-\tan\alpha\tan\beta\\ \cos(\alpha+\beta)&=&\cos\alpha\cos\beta(1-\tan\alpha\tan\beta)\\ &=&\cos\alpha\cos\beta-\sin\alpha\sin\beta\\ \end{array}$$
- 7,790
We can easily figure out that rotation of $\mathbf{R}^2$ by an angle $\theta$ is given by the linear transformation described by the matrix $ A = \begin{bmatrix}\cos\theta & -\sin\theta\\\ \sin\theta & \cos\theta\end{bmatrix}$.
Now, consider the vector $ V = \begin{bmatrix}\cos\phi\\\ \sin\phi\end{bmatrix}$ on the unit circle.
After the rotation $A$, $V$ gets transformed into $ \begin{bmatrix}\cos(\phi+\theta)\\\ \sin(\phi+\theta)\end{bmatrix} = A*V$
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ $=\begin{bmatrix}\cos\theta & -\sin\theta\\\ \sin\theta & \cos\theta\end{bmatrix}\begin{bmatrix}\cos\phi\\\ \sin\phi\end{bmatrix}$
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ $=\begin{bmatrix}cos\theta\cos\phi-\sin\theta\sin\phi \\\ \sin\theta\cos\phi+\cos\theta\sin\phi\end{bmatrix}$
Comparing the components we get $$\cos(\theta+\phi)= \cos\theta\cos\phi-\sin\theta\sin\phi$$ $$\sin(\theta+\phi) = \sin\theta\cos\phi+\cos\theta\sin\phi$$
- 2,381