2

Find a coordinate transformation diagonalizing the quadratic form.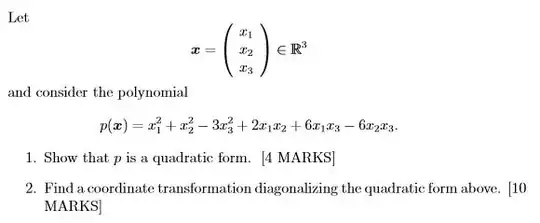enter image description here

Interesting in answering number 2. So, here is my approach:- Step 1:- Write the matrix representation of the equation, that is

A= 

       1  1  3
       1  1 -3
       3 -3 -3

Step 2: After doing this I then use a regular 3x3 matrix diagonalisation procedure. That includes finding the eigen values and vectors, and using this formula :- D=P^-1(A)P. Is that the right approach?

Mi-lee Wilson
  • 545

2 Answers2

3

Diagonalization of a matrix as a linear map is different from a diagonalization of a matrix as a quadratic form. $P^{-1}AP$ is the linear map diagonalization. For a quadratic form, consider the coordinate change $x=P\hat x$, then $p(x)=x^TAx=\hat x^TP^TAP\hat x$, that is we have $P^TAP$ diagonalization instead. It can be done by completing the squares in $p(x)$ or $LDL$ decomposition.

A.Γ.
  • 29,518
  • 1
    see http://math.stackexchange.com/questions/395634/given-a-4-times-4-symmetric-matrix-is-there-an-efficient-way-to-find-its-eige/1170390#1170390 where the OP thought it necessary to find eigenvalues, but all that is required is completing the squares (Hermite's method) or this slightly reversed method; the only real difference from Hermite is that one need not invert a matrix at the end – Will Jagy Nov 09 '15 at 17:21
2

When you complete the squares in $p(x)$ you will get $$ p(x)=(x_1+x_2+3x_3)^2-3(x_2+3x_3)^2+3x_2^2. $$ Then with $$ \tilde x=\pmatrix{1 & 1 & 3\\0 & 1 & 0\\0 & 1 & 2}x=Px $$ it becomes $$ A=P^T\pmatrix{1 & 0 & 0\\0 & 3 & 0\\0 & 0 & -3}P. $$

Nyfiken
  • 927