Why don't sine graphs consist of semicircles below and above the x-axis?

Question

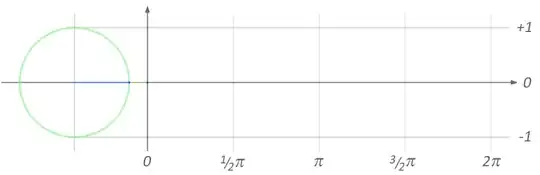
I'd like to see the flaw in my logic in the following:

I have a circle with radius 1. Therefore:

opposite side = sin(angle) = opposite / hypotenuse = opposite / 1

See this picture for a graphic depiction.

(Large version)

Therefore, the opposite sides (in green on the picture) when changing the x value from 1 to 0 will increase in height and their co-ordinates effectively mimic the circle's curve.

Because the height of these opposite sides equals the sine of the angles, these can be mapped onto a sine graph (x-axis is the angles in degrees, y-axis is opposite side height), and should replicate the circle's curve but mirrored. This means that sine graphs should have a semicircle shape above the x-axis from x values of 0-180 and a mirrored semicircle below the x-axis from x values of 180-360.

Where have I gone wrong?

When I look at a real sine graph I can't cut out the bottom section, slide it under the positive parabola and form a circle - but why not?

Answer 1

It's not standard to answer a question with an image, but I think the image says more than 1000 words in this case:

The point is that what you are drawing on the x axis is the angle, not the length of one of the sides of the triangle. The angle is proportional to the length of the circle section.

---

Image Source. Credit for the image goes to Lucas V. Barbosa.

Answer 2

You are treating the height as a function of the $x$ position of the base of that vertical leg. But $\sin$ is a function of the angle. Or alternatively, a function of how much circumference has been traced out. It's not (directly) a function of the $x$ position of that vertical segment.

Answer 3

Because the height of these opposite sides equals the sine of the angles,

OK, $\sin\alpha = y / 1 = y$ for one but $\cos\alpha = x / 1 = x$ for the other opposite site.

these can be mapped onto a sine graph (x-axis is the angles in degrees, y-axis is opposite side height),

OK. $F = (\alpha, y(\alpha)) = (\alpha, \sin(\alpha))$

and should replicate the circle's curve but mirrored.

You probably thought $(x, y(\alpha(x))$, where $$ y(\alpha(x)) = y(\arccos(x)) = \sin(\arccos(x)) = \sqrt{1-\cos(\arccos(x))^2} = \sqrt{1-x^2} $$ which is indeed an upper half circle.

My favourite cyclic animation is this one.

Use $2$ as the numeric parameter.

Answer 4

Because your blue line is cos(x) and your green line is sin(x). This reminds me of someone who forgot once that geodesics are taken at unit speed and spent the next two months trying to find the error in the equations.

Answer 5

I'm glad someone has my all life question too! I'm not alone in this world! I think I have an approximation to the answer please let me know what you think if you can. In this link https://www.desmos.com/calculator/7j6afasatg

I created there a comparison between sine function vs semicircle function like this: sin vs semicircle

The semicircle function is, if you analyze the equation, the variation of the length of one cathetus (of a right triangle with constant hypotenuse=1) when the length of the other cathetus varies. I mean the X axis is the size of one cathetus and Y is the length of the other cathetus. But the angle it's not there.

In Sine function the X axis is the angle (the angle is in radians: the length of the sub circumference for a given angle in a circle with radius=1, 180 degree is = PI length circumference).

In Sine function, Y axis, yes is the length of one cathetus as semicircle function. The X axis difference changes everything, because if you take one minute to imagine your finger walking through one circumference at constant velocity so you can imagine that the distance between your finger and X axis varies almost proportional with minor angles and almost no variation with bigger angles.

As always in Physics all is about Rhythm or velocity changes in time. And with Sine you are analyzing how are this changes with the "time" focused on the angle, and not in the size of other cathetus.