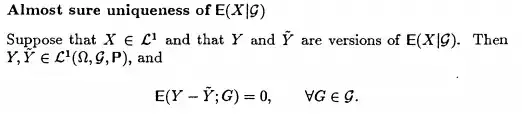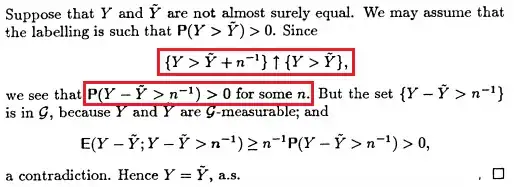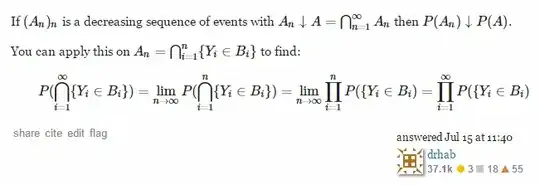Lemma about probability space P (From Grimmett and Stirzaker)

Question

This is from Grimmett and Stirzaker, Chapter 1, page 7.

Lemma. Let $A_{1},A_{2},...$ be an increasing sequence of events, so that $A_{1}\subseteq{A_{2}}\subseteq{A_{3}}\subseteq{...}$, and write A for their limit:

$A=\bigcup\limits_{i=1}^{\infty}{A_{i}}=\lim_{i\to\infty}{A_{i}}$

Then, $P(A)=\lim_{i\to\infty}{P(A_{i})}$

Proof.

$A={A_{1}}\cup({A_{2}-A_{1}})\cup({A_{3}-A_{2}})\cup{...}$ is a disjoint union of sets. Thus, by definition,

$P(A) = P({A_{1}})+\sum_{i=1}^{\infty}P({A_{i+1}}\setminus{A_{i}})$

$P(A) = P({A_{1}})+\lim_{n\to\infty}\sum_{i=1}^{n-1}(P({A_{i+1}})-P({A_{i}}))$

$P(A)=\lim_{n\to\infty}{P(A_{n})}$

Whilst I understand the math behind the proof, what are we trying to prove here. Why would be interested in such an increase sequence of events? What good is this result?

Answer 1

Some examples:

1. Used in the proof of $P(\liminf A_n) \le \liminf P(A_n) \le \limsup P(A_n) \le P(\limsup A_n):$

$$P(\liminf (A_n)) = \lim_{N \to \infty}P(\bigcap_{n \ge N} A_n)$$

---

2. Uniqueness of conditional expectation (Williams' Probability w/ Martingales)

---

---

---

3. From Rosenthal's book:

---

---

4. A property of independence of random variables

---

---

5. Continuity of 'measure' proves countable additivity:

---

---

6. Another example