Find the complex (or real) roots of $e^{\frac{3 x}{2}}+2 \cos \left(\frac{\sqrt{3} x}{2}\right)$

Question

Define for natural $n\geq 2$ $$G(x,n)= \sum _{k=0}^\infty \frac{x^{k n}}{(k n)!}= \frac{\sum _{k=0}^{n-1} e^{x e^{\frac{2 i \pi k}{n}}}}{n}= G(x e^{\frac{2 i \pi}{n}},n)= \prod_{m=1}^\infty \left(1+\left(\frac{x}{r(n,m)}\right)^n\right) $$ where $r(n,m)$ is the $m$th biggest absolute value of a root of $G(x,n)$.

The complex roots for $G(x,2)$ and $G(x,4)$ are trivial to find. $r(2,m)=\left(m-\frac{1}{2}\right)\pi$ and $r(4,m)=\left(m-\frac{1}{2}\right)\pi\sqrt{2}$.

Because of rotational symmetry $G(x,3)=G(x e^{\frac{2 i \pi}{3}},3)$, we only need to find the roots on the real line. Note that $$G(x,3)=\frac{1}{3} \left(e^x+2 e^{-\frac{x}{2}} \cos \left(\frac{\sqrt{3} x}{2}\right)\right)$$ From this we can see that as $x\rightarrow -\infty$, the roots of $G(x,3)$ become arbitrarily close to the roots of $\cos \left(\frac{\sqrt{3} x}{2}\right)$

Because of this, we can use Newton's Method to find the roots of $G(x,3)$ by starting with the roots of $\cos \left(\frac{\sqrt{3} x}{2}\right)$.

The Mathematica code for $r(3,m)$ is

-x /. FindRoot[E^(3 x/2) + 2 Cos[(Sqrt[3] x)/2], {x, -2 Pi (-1/2 + m)/Sqrt[3]}]

This is not good enough though. I desire a formula for $r(3,m)$ which does not not involve a FindRoot. Also, because you could define Newton's method exactly with a limit, limits are not allowed in the final formula.

Because of input from the comments, we now have a new formula for $r(3,m)$: $$\frac{\pi(2m-1)}{\sqrt{3}}-\sum _{n=1}^{\infty } \frac{\left(-e^{\frac{1}{2} \sqrt{3} (\pi -2 \pi m)}\right)^n \left(\lim_{x\to \frac{\pi -2 \pi m}{\sqrt{3}}} \, \frac{\partial ^{n-1}}{\partial x^{n-1}}\left(\frac{x-\frac{\pi -2 \pi m}{\sqrt{3}}}{-e^{\frac{1}{2} \sqrt{3} (\pi -2 \pi m)}+e^{\frac{3 x}{2}}+2 \cos \left(\frac{\sqrt{3} x}{2}\right)}\right)^n\right)}{n!}$$ Though Mathematica cannot calculate this, the corresponding Mathematica code is:

-(([Pi] - 2 m [Pi])/Sqrt[3]) - Sum[(-E^(1/2 Sqrt[3] ([Pi] - 2 m [Pi])))^n/n!* Assuming[{Element[m, Integers]}, Limit[D[((x - ([Pi] - 2 m [Pi])/Sqrt[3])/(E^(3 x/2) + 2 Cos[(Sqrt[3] x)/2] - E^( 1/2 Sqrt[3] ([Pi] - 2 m [Pi]))))^n, {x, n - 1}], x -> ([Pi] - 2 m [Pi])/Sqrt[3]]], {n, 1, Infinity}]

The remaining work is to find the general $(n-1)$th derivative in the sum and to get rid of the limit in the sum.

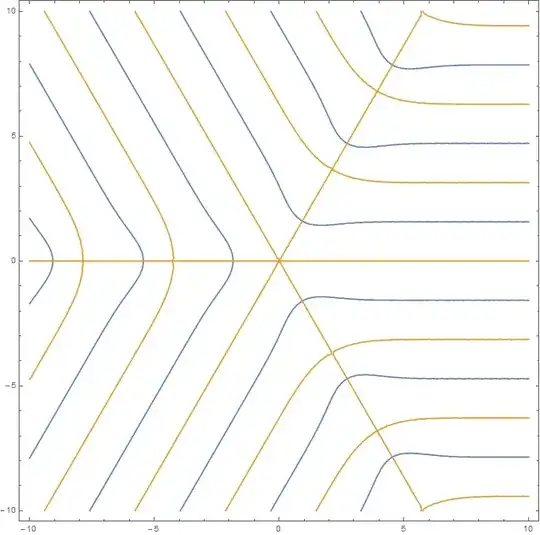
Here is a contour plot showing the roots of $G(x,3)$. The orange curve is $\Im(G(x,3))=0$. The blue curve is $\Re(G(x,3))=0$. The plot shows $-10<\Re(x)<10,-10<\Im(x)<10$.

Also, by comparing the sum and product forms of $G(x,n)$, we can see $$ \frac{1}{n!}=\sum_{m=1}^\infty\frac{1}{r(n,m)^n}$$

Answer 1

If we look for the real zeros of function $$f(x)=\cos(x)+\frac{1}{2}e^{x\sqrt 3}$$ expanding as a Taylor series around $x=-(2n+1)\frac \pi 2$, limited to $O\left(\left(x+\frac{1}{2} \pi (2 n+1)\right)^4\right)$and using power series reversion,we have $$x_n=-(2n+1)\frac \pi 2-$$ $$\frac{99+176 \sqrt{3} (-1)^n T+472 T^2+192 \sqrt{3} (-1)^n T^3+96 T^4 }{ 6 \left(\sqrt 3+2 (-1)^n T\right)^5}$$ where $$T=\exp\left( \frac{(2n+1)\sqrt{3}\pi}{2} \right)$$

$$\left( \begin{array}{ccc} n & \text{estimate} & \text{solution} \\ 0 &\color{red}{ -1.6019848}34730162686632007 & -1.601984876344266726648546 \\ 1 & \color{red}{-4.712246313369723861}742906 & -4.712246313369723861642345 \\ 2 & \color{red}{-7.853982252057236748320048} & -7.853982252057236748320048 \\ \end{array} \right)$$

Answer 2

Too long for a comment .

The real zero :

For an iterative method with quick convergence as $\cos(x)<0$ see Exercise for student about $y\simeq P$

Some details :

Let :

$$\frac{2}{3}x\left(\frac{9}{16}\left(\frac{2}{3}x+1\right)+\frac{\left(\frac{15}{9}+\frac{16}{9}y\right)\frac{9}{16}}{1+\frac{2}{3}x}\right)-y+\frac{x^{4}}{4\left(4x+6\right)}+\frac{x^{5}}{5}\cdot\frac{1}{4\left(4x+6\right)}=\frac{x^{5}+5x^{4}+20x^{3}+60x^{2}+120x-120y}{80x+120}$$

Let :

$$f_a(x)=\ln\left(\frac{a}{\frac{2}{3}\left(\frac{9}{16}\left(\frac{2}{3}x+1\right)+\frac{\left(\frac{15}{9}+\frac{16}{9}a\right)\frac{9}{16}}{1+\frac{2}{3}x}+\frac{2}{3}\frac{x^{3}}{4\left(4x+6\right)}+\frac{3}{2}\frac{x^{4}}{5}\cdot\frac{1}{4\left(4x+6\right)}+\frac{x^{5}}{4\cdot5\cdot6\left(4x+6\right)}\right)}\right),a=\left|2\cos\left(\frac{\sqrt{3}}{2}b\right)\right|,h(x)=e^{\frac{3}{2}x}-\left|2\cos\left(\frac{\sqrt{3}x}{2}\right)\right|,g\left(x\right)=f_a\left(\frac{3}{2}x\right)$$

Then one can show that for example where $a=b_k<0$ is a root for the problem:

Step 1 :

$$h'(y)(b_{k}-y)+h(y)\simeq f_{{b_k}}(y) $$

Then if :

$$h'(y)(b_{k}-y)+h(y)=h(x)$$

Have strictly more than two solution come back to to step 1) with the new value

Step 2)

If it have two solution determine :

$$h'(y)(b_{k}-y)+h(y)=0$$

Come back to step 1)

It gives a new approximated solution

It's like Newton's method .

Answer 3

Substitute and rearrange: $$\cos\left(\frac{\sqrt3z}2\right)+\frac12 e^{\frac{3z}2}=0\mathop\iff^{z=\frac{2x}{\sqrt3}}\cos(x)+\frac12 e^{\sqrt3 x}=0\mathop\iff^{x=\ln(w)} w^{2i}+w^{\sqrt3+i}+1=0$$

then substitute $w^{2i}=u\iff w=u^\frac1{2i}e^{\pi k},k\in\Bbb Z$, apply Lagrange reversion, and use factorial power

$$w^{2i}+w^{\sqrt3+i}+1=0\iff u=-1-e^{(\sqrt3+i)\pi k}u^{\sqrt[-3]{-1}}\implies x_k=\pi k-\frac i2\ln(u_k)=\pi k-\frac i2\ln(-1)-\frac i2\sum_{n=1}^\infty\frac{\big(-e^{(\sqrt3+i)\pi k}\big)^n}{n!}\left.\frac{d^{n-1}}{dt^{n-1}}\ln’(t)t^{\sqrt[-3]{-1}n}\right|_{-1}=\left(k+\frac12\right)\pi-\frac i2\sum_{n=1}^\infty\frac{e^{\sqrt[6]{-1}(2k+1)\pi n}}{n!}(\sqrt[-3]{-1}n-1)^{(n-1)}$$

Combining this result, the root’s three-fold symmetry, and substituting $k\to-k$ gives:

$$\bbox[2.5px,border: 3px blue solid]{\cos\left(\frac{\sqrt3z}2\right)+\frac12 e^{\frac{3z}2}=0\implies z_{m,k}=\frac{(-1)^\frac m3(1-2k)\pi}{\sqrt3}-\frac {i(-1)^\frac m3}{\sqrt3}\sum_{n=1}^\infty \frac{e^{\sqrt[6]{-1}(1-2k)\pi n}}{n!}(\sqrt[-3]{-1}n-1)^{(n-1)};k\in\Bbb N,m=0,1,2}$$

where the series matches the actual roots. If $n=0$, the series diverges so the Fox Wright function cannot easily be used. Also, if all of its parameters were extended to complex numbers and the $n=0$ problem were gone, then Fox Wright would give a closed form.