2

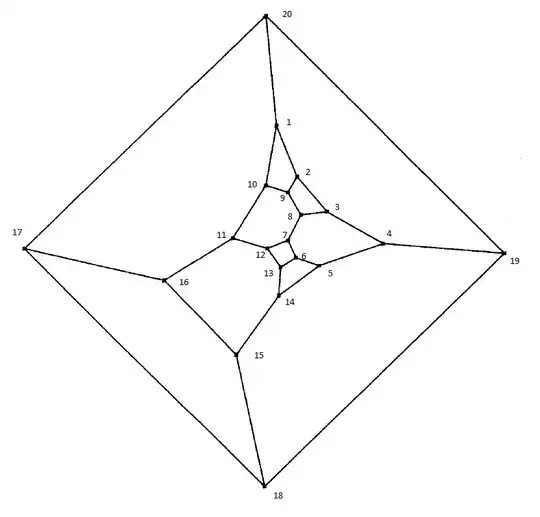
Below you see an example of a bicubic graph consisting of faces with degree $4$ and $6$, which makes up the set of graphs of my interest, called Barnette graphs.

enter image description here

Some more examples, including this, are given in DeLaTorre's "Investigation of Barnette's Graphs". The list of examples stop at $20$ vertices. As you easily spot the six squares are grouped in pairs: $\{(1,2,9,10),(2,3,8,9)\},\{(5,6,13,14),(6,7,12,13)\},\{(15,16,17,18),(17,18,19,20)\}$

How many vertices do you need so that all squares are not directly connected?

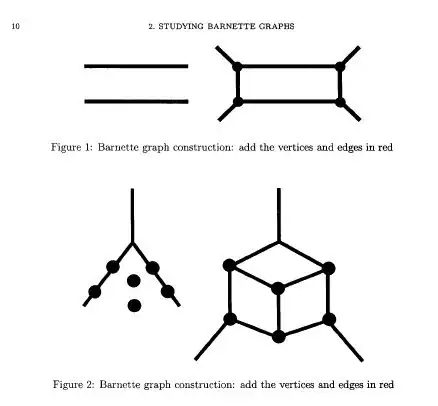
As the cited Horton-Manvel-McKay theorem states: "Every Barnette graph can be generated up to isomorphism using the two operations shown"

$\hskip1.0in$enter image description here

But I don't see how to use these operations to separate the squares finally...

Community
  • 1
draks ...
  • 18,449
  • 1
    I'm kinda sad because the captions in those images say "... add the vertices and edges in red", but the images are black-and-white. – Mike Pierce Nov 28 '15 at 03:28
  • @MikePierce I'm sorry. This is a screenshot of a black and white paper. Colors were not supported, so use your imagination... – draks ... Dec 02 '15 at 11:05

1 Answers1

2

The answer is $20$: Truncated octahedron;

enter image description here

draks ...
  • 18,449