How do I get $ \int_0^1 \frac{dz}{\sqrt{z(z - 1\,)(z+1\,)}} = \frac{\sqrt{\pi}}{2} \frac{\Gamma(\frac{3}{4})}{\Gamma(\frac{9}{4})}$?

Question

While reading physics papers I found a very interesting integral so I decided to write it down. Let $p(z) = z^ 3 - 3\Lambda^ 2 z$ where $\Lambda$ could be any number. If you want $\Lambda = 1$ and $p(z) = z^ 3 - 3z$. Then

$$ \int_0^{\sqrt{3}\Lambda} \frac{dz}{\sqrt{p(z)}} = \int_0^{\sqrt{3}\Lambda} \frac{dz}{\sqrt{z(z - \sqrt{3}\Lambda\,)(z+\sqrt{3}\Lambda\,)}} = \frac{\sqrt{\pi}}{2} \frac{\Gamma(\frac{3}{4})}{\Gamma(\frac{9}{4})} (\sqrt{3}\Lambda)^{5/2}$$

The physics paper at least tell us $\int \propto \Lambda^{5/2}$ so we know the growth rate. It could be that $\Lambda = \frac{1}{\sqrt{3}}$ is even simpler than $\Lambda = 1$.

$$ \int_0^1 \frac{dz}{\sqrt{z(z - 1\,)(z+1\,)}} = \frac{\sqrt{\pi}}{2} \frac{\Gamma(\frac{3}{4})}{\Gamma(\frac{9}{4})}$$

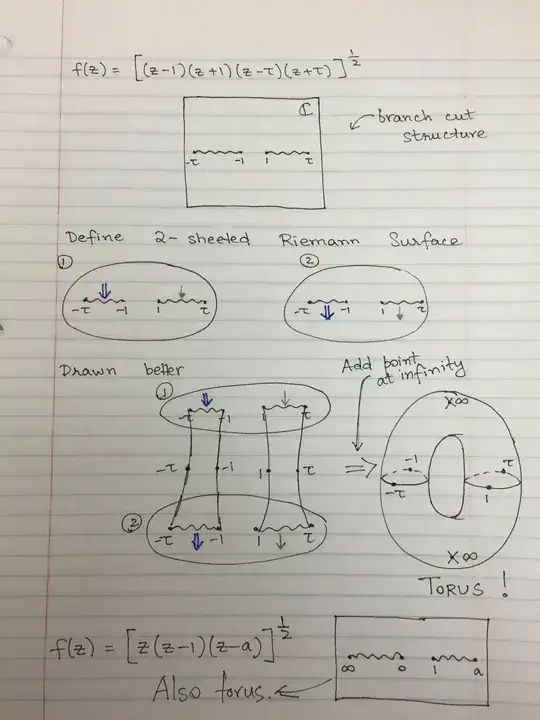
This should be connected to the Riemann surface $y^ 2 = z(z^2 -1)$. And we are computing a period of the Riemann surface.

Contour integration is really important here. Checking on Wolfram Alpha gives a different answer:

$$ \int_0^1 \frac{dz}{x(x^2-1)} = - 2i\sqrt{\pi}\,\frac{ \Gamma(\frac{5}{4})}{\Gamma(\frac{3}{4})}$$

I am guessing this is either the same number or Mathematica is choosing a different contour. Physicists love contour integrals (taken from physics.stackexchange):

Alpha's answer can't be right - $\Gamma(\frac54)$ and $\Gamma(\frac34)$ are both real, so Alpha's expression is pure imaginary, but the integral is patently real. — Steven Stadnicki, Dec 21 '15 at 23:55
@StevenStadnicki Alpha's answer is correct, the integral is plainly imaginary because $(z^2-1) < 0$ on $(0,1)$. — achille hui, Dec 21 '15 at 23:56
@achillehui D'oh - I was looking at the second expression which is missing the square root. You're 100% right, of course. — Steven Stadnicki, Dec 21 '15 at 23:58
It looks to me like $\int \propto \Lambda^{-1/2}$, not $\Lambda^{5/2}$. — Barry Cipra, Dec 22 '15 at 00:13
@cactus314, I assume you mean eq 3.22. Please see my answer below. — Barry Cipra, Dec 22 '15 at 04:02

score 2 · Accepted Answer · answered Dec 21 '15 at 23:57

Since: $$\int_{0}^{1}x^{\alpha-1}(1-x)^{\beta-1}\,dx = B(\alpha,\beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}\tag{1}$$ through a change of variable we get:

$$ \int_{0}^{1} z^{-1/2}(1-z^2)^{-1/2}\,dz = \frac{1}{2}\int_{0}^{1}z^{1/4}(1-z)^{-1/2}\,dz = \frac{\Gamma\left(\frac{5}{4}\right)\Gamma\left(\frac{1}{2}\right)}{2\cdot \Gamma\left(\frac{7}{4}\right)}\tag{2} $$ and by using the reflection formulas for the $\Gamma$ function that simplifies to:

$$ \int_{0}^{1} \frac{dz}{\sqrt{z(1-z)(1+z)}} = \color{red}{\frac{\Gamma\left(\frac{1}{4}\right)^2}{2\sqrt{2\pi}}}.\tag{3}$$

I found this similar problem http://math.stackexchange.com/questions/867676/prove-int-0-infty-left-sqrt1x4-x2-right-dx-frac-gamma2-le?rq=1 — cactus314, Dec 22 '15 at 17:07

score 0 · Answer 2 · answered Dec 22 '15 at 04:01

In comments, the OP gave a reference for the source of the equation. But the equation there is

$$-2\int_{-3\Lambda}^0dz\sqrt{p(z)}=-\frac{\sqrt{\pi}}{2} \frac{\Gamma(\frac{3}{4})}{\Gamma(\frac{9}{4})} (\sqrt{3}\Lambda)^{5/2}$$

The crucial difference is that $\sqrt{p(z)}$ is in the numerator, not the denominator, of the integral.

How do I get $ \int_0^1 \frac{dz}{\sqrt{z(z - 1\,)(z+1\,)}} = \frac{\sqrt{\pi}}{2} \frac{\Gamma(\frac{3}{4})}{\Gamma(\frac{9}{4})}$?

2 Answers2