4

I have a function that includes the phrase $(-x)^{1/3}$. It seems like this should always evaluate to $-(x^{1/3})$. For example, $-1 \cdot -1 \cdot -1 = -1$, so it seems that $(-1)^{1/3}$ should equal $-1$.

When I plug $(-1)^{(1/3)}$ into something like Mathematica, I get: 

0.5 + 0.866025i

Cubing this answer does in fact compute to $-1$.

Is this a situation, like $\sqrt4$, where there are two valid answers , $\{-2, 2\}$?

Antonio Vargas
  • 24,993
Chris Wilson
  • 283
  • For the $\sqrt{4}$, the only "answer" is $2$. However, for $x^2=4$, the equation is satisfied by $\pm 2$. – zz20s Jan 06 '16 at 16:09
  • $\sqrt{4}$ has only one answer, namely $2$. $4^{\frac{1}{2}}$ on the other hand has two answers. $\sqrt{4}$ and $4^{\frac{1}{2}}$ are two completely different notations meaning two different things. – JMoravitz Jan 06 '16 at 16:10
  • Every number has two square roots ($\sqrt a$ and $-\sqrt a$). Every number also has three (possibly complex) cube roots, four (possibly complex) fourth roots, etc. – Akiva Weinberger Jan 06 '16 at 16:18
  • The three cube roots of $1$ are: $1$, $-\frac12+i\frac{\sqrt3}2$, and $-\frac12-i\frac{\sqrt3}2$. It turns out that, when you draw them on the complex plane, they are the corners of an equilateral triangle. (The cube roots of $-1$ are the negatives of these.) – Akiva Weinberger Jan 06 '16 at 16:21
  • I suggest you take a look at:https://en.wikipedia.org/wiki/Cube_root – NoChance Jan 06 '16 at 16:40
  • Since you refer to Mathermatica, use the function Surd. "Surd[x, n] gives the real-valued n^th root of x." – Bob Hanlon Jan 06 '16 at 17:04

2 Answers2

5

The end result is that $x^y$ is technically a multi-valued function whenever $y$ is not an integer. This is often overlooked in favor of considering only the principal root (smallest argument greater than or equal to zero) as is the case with the square root (which will result in real numbers only in the case that $x$ is a non-negative real number). In the further case that $y$ is an irrational number, then there are infinitely many solutions.

Here, I will attempt to go into more detail about the case where $y$ is a simple fraction with $1$ as the numerator.

De Moivre's Theorem for fractional powers: for a complex number in polar form with $r$ a non-negative real number, one has $$(r(cos\theta+i\sin\theta))^{\frac{1}{n}}=\sqrt[n]{r}\left[\cos\left(\frac{2k\pi+\theta}{n}\right)+i\sin\left(\frac{2k\pi+\theta}{n}\right)\right]~~\text{for}~k=0,1,2,\dots,n-1$$

Graphically, if one were to want to find the results of $z^{\frac{1}{n}}$ for some complex number $z$, plot it on the complex plane. Take the magnitude of $z$ and replace it with the magnitude of $\sqrt[n]{|z|}$. Take the angle of $z$ and replace it with $\frac{1}{n}$ of that angle. From there, draw a regular $n$-gon with one of the points being the just found point. All of the corners will be the solutions.

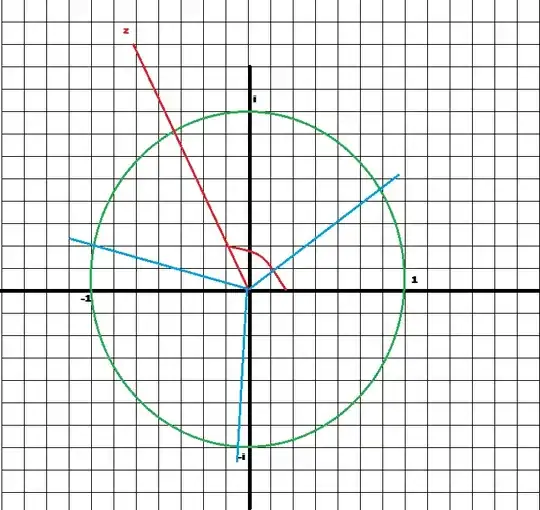
roots

Pictured above is the original number $z$ (in red), and its three cube roots (in blue).

Community
  • 1
JMoravitz
  • 79,518
1

Use $e^{i\pi}=-1$. Then $(e^{i\pi})^{1/3}=e^{i\pi/3}=-1^{1/3}$

De Moivre's gives $e^{i\theta}=\cos(\theta)+i\sin(\theta)$

If $\theta=\frac{\pi}{3}$, then it follows that

$(-1)^{1/3}=e^{i(\pi/3)}=\frac12+\frac{i\sqrt3}{2}\approx0.5 + 0.866025i$

Minion Jim
  • 105
JMP
  • 21,771
  • Thanks! For my purposes, I only want the real solution among the three possible valid solutions. Is there a way to force that? – Chris Wilson Jan 06 '16 at 16:26
  • 1
    there are k-roots of $-1^{1/k}$ - most Math software returns the $1^{st}$. View this as $-1^{j/k}$ to get the $j^{th}$ root and $-1$ is the $k^{th}$ root – JMP Jan 06 '16 at 16:31