The comments on the previous (correct) answer suggest that the Voronoi sites are unique if there is at least one Voronoi vertex. Here are some examples that show that the sets may not be unique even in that situation.
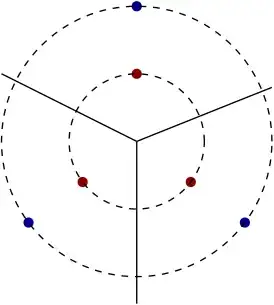
If there are just three Voronoi cells meeting at a single Voronoi site, there are a family of point sets generating this Voronoi diagram: the three sites can live on any circle centered at the Voronoi vertex. Below, the three red points and the three blue points generate the same Voronoi diagram.
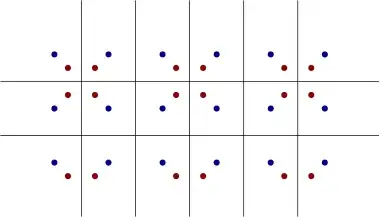
For points that are not in general position (i.e., four points can lie on a circle), there are larger examples where the same Voronoi diagram is generated with different point sets. For example, the blue points below form a Voronoi diagram of a regular square grid. The red points also which have been alternatively offset in opposite directions also generate the same grid.
If the points are in general position and there are at least two Voronoi vertices in the Voronoi diagram, then the problem seems to be constrained enough to ensure the Voronoi sites are unique.

