What does the notation "*" mean?

Question

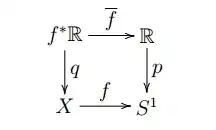
I do not know the name of or what it does so I have no means of searching for an answer over the internet or a book. In my notes for algebraic topology, I have this bit that says,

For any $f: X \rightarrow S^1$, define $\bar{f}: f^* \mathbb{R} \rightarrow \mathbb{R}$ and $q:f^* \mathbb{R} \rightarrow X$.

I don't know what the space or set $f^* \mathbb{R}$ is supposed to mean, namely what "*" means either as a symbol or as some operator. Is it equvialent to $f(\mathbb{R})$?

I've searched through my past notes but cannot find something that explains it, is anyone familiar with the notation?

Edit The question follows,

Prove that the following diagram commutes. Namely, show that $p o \bar{f} = \bar{f} o q: f^* \mathbb{R} \rightarrow S^1$

Upper star usually means pullback. I think it might also be used for induced maps on homotopy/homology. — Future, Feb 02 '16 at 18:19
I agree with the two previous comments. Usually (but not always) $f^$ is the pullback and $f_$ the pushforward of an operator. — Dan, Feb 02 '16 at 18:20
hi guys, thanks for answering. To make sure, i'll add the whole question then — John Trail, Feb 02 '16 at 18:22

score 4 · Accepted Answer · edited Apr 13 '17 at 12:19

This is most probably the pullback of the covering map $\mathbb{R} \to S^1$. In a more general context, suppose that $p : E \to B$ is some covering space, and $f : X \to B$ is any continuous map. Then the linked Q&A shows that $$f^*E := E \times_B X = \{ (e,x) \in E \times X \mid p(e) = f(x) \}$$ is a covering space via the projection $q : f^* E \to X$, and there is also a projection $\bar{f} : f^* E \to E$ such that the diagram commutes ($p \circ \bar{f} = f \circ q$).

Since you're asked to prove that $p \circ \bar{f} = f \circ q$, you probably have another definition of the pullback (because it is immediate with the definition I've given), and we cannot just guess what it is. You'll have to search your notes more thoroughly.

What does the notation "*" mean?

1 Answers1